What is DFT + embedded DMFT Functional (eDMFT)

eDMFT is a software package implementing the combination Density Functional Theory [1] and Dynamical Mean Field Theory [2, 3], which is derived from the stationary Luttinger-Ward functional [4]. The implementation is carefully designed so that it keeps the stationarity of the original functional throughout the algorithm, and postulates the locality of the correlations in real space [5], as opposed to more commonly chosen locality of correlations in Wannier space. The single-particle Green’s function is expanded in the full potential LAPW basis, and the single-particle Green’s function is self-consistently determined (including self-consistent electronic charge). The algorithm also implements the exact double-counting of DFT and DMFT [6]. The impurity solvers include numerically exact continuous time quantum Monte Carlo [7], non-crossing and one-crossing approximation [8].

Current features and capabilities of eDMFT are listed below:

• total free energy and forces in the presence of strong correlations
• exact double-counting of DMFT and LDA
• non-collinear magnetism
• theoretical spectroscopies, such as optics, resistivity, neutron structure factor, resonant elastic X-ray scattering
• several solvers: continuous time quantum Monte Carlo, NCA, OCA
• extreme parallelism (scales up to 100,000 cores) using Message Passing Interface (MPI)
• parallel execution by OpenMP

eDMFT is a flavor of so called DFT+DMFT method, however, in literature DFT+DMFT usually referes to an algorithm whereby DFT is used to determine tight-binding model with the corresponding Wannier orbitals, which are then used to solve a generalized Hubbard model (or sometimes Anderson type lattice model) within DMFT.

DFT+DMFT was first introduced using such downfolding technique [9, 10], but was later put on more firm footing by defining the stationary functional which combines the two approximations [3]. eDMFT implements one variant of such functional, which is described below.

The existence of such stationary functional is important for stable implementation of the algorithm, because only if the functional exists and is stationary, the implementation is robust, and small error in practical computation leads to negligible error in the final result. For example, in DFT the total energy has second order error in prime variable of interest, the density. Similarly, here the free energy has second order error in the local and static component of the Green’s function.

Notice also that eDMFT implementation does not approximate the itinerant states (or any state) within the tight-binding approximation, rather all valence states are described in the LAPW basis and are allowed to hybridize with the correlated localized subset. The correlated subset, projected to by the projector, is treated dynamically, while the rest of the states are treated at the static mean field level by the DFT, but not removed from the model nor approximated by tight-binding model.

More precise definition of DFT+eDMFT Functional

Luttinger-Ward functional

To compare and combine methods, it is useful to cast them in the same functional language, and perhaps the best choice is the Luttinger-Ward (LW) functional of the form

DFT within Luttinger-Ward approach

Within the density functional theory (DFT), the prime variable of interest is the electron density ρ(r). The DFT theory in the Luttinger-Ward language is obtained by approximating Φ[{G}] by the Hartree and exchange correlation energy functional, i.e., Φ[{G}] = E_H[ρ] + E_xc[ρ]. The extremization of the LW functional leads to the well known DFT equations (G^-1 = G ₀^-1 - V _H - V _xc), which map the many-electron problem onto a single-electron problem in an effective potential (V _KS = V _H + V _xc). Although the exact DFT gives exact total energy and therefore exact value of the free energy Γ at zero temperature, DFT in the Luttinger-Ward approach appears as an approximation, which delivers an approximation for the single-particle Green’s function, and therefore DFT band-structure is seen as the approximation to the true excitation spectra.

Within local density approximation (LDA), the form of the exchange-correlation functional is purely local in 3D space, given by E_xc[{ρ}] = ∫ d³rρ(r)ε _xc[ρ(r)], where ε_xc(n) is a function of density, determined from the auxiliary system, namely the electron gas. The correlation potential within LDA is then a simple function of ε_xc(n), and is given by V _xc = δE_xc∕δρ = ε_xc + ε_xc′ρ. We hence conclude that in order to determine the correlation potential within LDA, each point in space is mapped to an auxiliary problem of electron gas, and each point in space is treated as independent in this step. It is due to the kinetic energy, the Hartree part of the Hamiltonian and the Dyson equation that different points in space get coupled, and the band structure with momentum dependence appears. As the DFT band structures in most weakly correlated materials are reasonable, we can conclude that even purely local approximation on LW functional Φ[{G}] (an approximation in which each point in space is independently mapped to an auxiliary problem) is a reasonable starting point. This extreme locality of the exchange-correlation functional in real materials is the reason for the extraordinary success of approximate DFT functionals such as LDA or GGA.

DMFT within Luttinger-Ward approach

DMFT was originally developed [2] in the context of the Hubbard model considering the limit of large dimensions [12] (or connectivity), where DMFT becomes exact. The DMFT approximation can also be cast into an extremizing problem of the LW functional, in which Φ[{G}] is approximated by the local functional Φ[{G_local^R}], but in DMFT the locality to the given site on the lattice R is enforced, rather than locality to a given point in 3D space. In addition, the functional form of Φ^DMFT is kept the same as the exact Φ[{G}], except that the variable of interest is truncated from the G(r,r′) to G_local(r,r′). Namely, G_local(r,r′) is the local component of G and vanishes when r and r′ are on different atoms. Due to the fact that Φ^DMFT is so closely connected to the exact functional, it must be dynamic, and it develops a singularity at sufficiently strong Coulomb interaction, as envisioned by Mott in 1930 [13, 14]. Mathematically, one can write the DMFT functional as

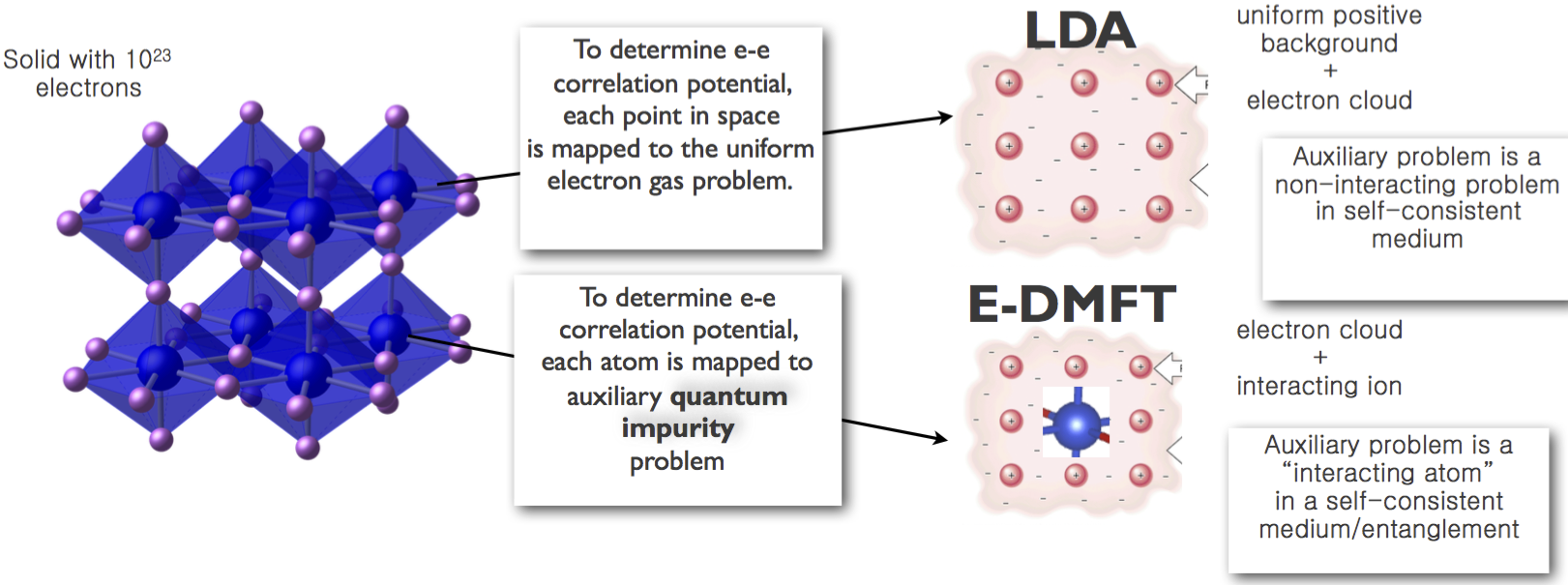
Notice the similarity of the two local approximations, LDA and DMFT, in which the LDA functional can be expressed by Φ_LDA^XC = ∫ d³rΦ^xc[G(rt,r′t′)δ(r - r′)δ(t-t′)] and the DMFT by Φ_DMFT ^XC = ∑ _RΦ^xc[G _local^R]. Both thus truncate the observable of interest in real space, as shown in Fig. 2, but LDA is local to a point in 3D space, while DMFT is local to an atom in the lattice. Notice also that the LDA functional delivers the exact energy and the exact charge density in the limit of uniform density, while DMFT gives the exact solution in the limit of large lattice connectivity, not just the ground state, but also the exact excitations. While the form of the wave function of the DMFT problem is not known, one can nevertheless compute any correlation function of the system, which can be computed with the impurity solver.

DFT+eDMFT Functional

Finally, the combination of DFT and eDMFT approximates the Φ[{G}] functional with the combination of DFT and DMFT terms Φ^LDA[{G}] + Φ^DMFT [{G}] - Φ^DC[{G}]. In principle one can define the DMFT-type approximation which would treat on the DMFT level all degrees of freedom [15], but current impurity solvers can not treat much more than seven orbitals (an open f shell), therefore a good choice is to treat more itinerant degrees of freedom on the DFT level, and add all Feynman diagrams only for those narrow orbitals in which correlations are strongest. Mathematically, the LW functional to be extremized is

In order to fully define the DFT+DMFT approximation, one needs to specify the projector to the local Green’s function, i.e., G_local^R = 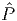^RG. Most early DFT+DMFT implementations used the Wannier basis constructed from a minimal set of bands, and mapping the problem to a Hubbard-like model. It was later shown  [5, 17, 18], that a better choice for DMFT projector is a real space projector, constructed by set of quasiatomic orbitals, which are much more localized than the Wannier orbitals, and for which the negligence of intersite correlations is much less severe. This is because correlations in real space are very local, but they are not necessary local in Wannier basis.

In order to preserve stationarity of the DFT+DMFT functional, the projector must be independent of the self-consistent charge density, therefore it needs to be fixed during the DMFT optimization. We recommend the following choice for the projector

Notice that in such formulation of DFT+DMFT, all valence states are kept in the model and are allowed to hybridize with the correlated localized subset. The correlated subset, projected to by the projector, is treated dynamically, while the rest of the states are treated at the static mean field level by the DFT, but not removed from the model. Moreover, the screened Coulomb repulsion Û among the electrons in such a real space projectors is larger and more universal among similar classes of materials [18].

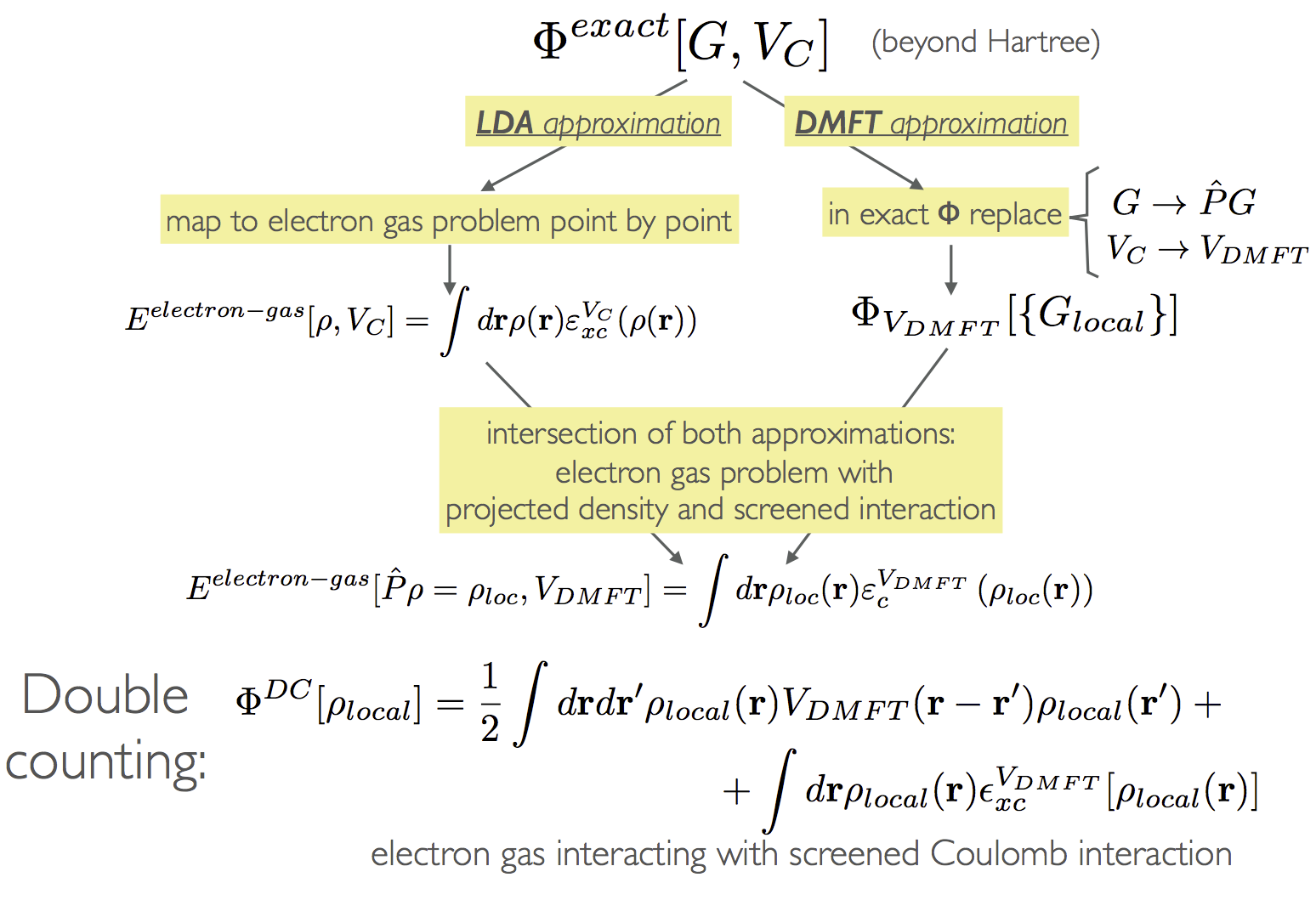
Exact double-counting : The double-counting problem arises from the fact that DFT (in its approximations such as LDA or GGA) and the DMFT, each contain some form of correlations, but what exactly is contained in both approximations was considered unknown. Several simplistic approximations derived in the context of LDA+U, and obtained in certain limits such as localized limit or mean-field limit, were used in practice.

In Refs. [6, 19] the exact overlap between the dynamical mean field theory and the band structure methods was derived quite generally using the Luttinger-Ward functional language introduced above. The basic idea is that Φ^DMFT and Φ^LDA in Eq. 3 are two different approximations of the same exact LW functional Φ^exact, and we know exactly how to get from Φ^exact to Φ^DMFT or to Φ^LDA. To obtain the LDA approximation, we truncate in Φ^exact the Green’s function to its static and local part, i.e., ρ(r) = G(rr′)δ(r - r′)δ(τ - τ′), hence the charge is the observable, and then map each point in space to the problem of electron gas. To get the DMFT approximation, we truncate in Φ^exact the Green’s function to the following local component G_loc(r,r′) = 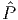G(r,r′) = ∑ _α,β ⟨r|ϕ_α⟩⟨ϕ_α|G|ϕ_β⟩⟨ϕ_β|r′⟩, and also replace the bare Coulomb repulsion v_C(r,r′) = 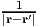with the screened Coulomb repulsion v_DMFT (r,r′) ( which obeys U_αβγδ = ⟨ϕ_αϕ_β|v_DMFT |ϕ_γϕ_δ⟩). To obtain the overlap between the two approximations, one can apply first the LDA approximation on the exact functional

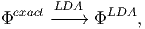(5)

and then apply the DMFT approximation

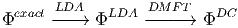(6)

to obtain the double-counted correlations. Alternatively, one can first start with DMFT approximation and then apply the LDA approximation to it

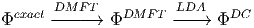(7)

and also get the same functional. The double-counted functional can be written as

Figure 2: The sketch of how to obtain the exact double-counting of the exchange functional within the Luttinger-Ward approach.

Figure 3: The sketch of how to obtain the exact double-counting of the correlation functional.

Total Free Energy and Forces : One possible way to compute the total energy of the system, is to use so-called Migdal-Galitskii formula to compute the DMFT potential energy (E_DMFT ^M-Galitskii = Tr(ΣG)) which can then be added to the LDA/GGA total energy. The total energy expression in this approach reads

However, within eDMFT functional approach, the free energy of the system is given by the LW functional:

Real usefulness and power of the free energy functional expression is evident for the calculation of forces. The force is defined as the change of the total energy when an atom is displaced F = -δE∕δR. The availability of forces on all atoms is essential for structural relaxations, and for computing phonons. Prior attempt to compute forces within DFT+DMFT was based on differentiating E_LDA+DMFT ^M-Galitskii. The problem is that in this case the force contains a term, which requires one to compute the two-particle vertex function (Γ_V = δΣ∕δG), which depends on three frequencies and four orbital indices, which is numerically extremely hard to compute.

The exact force at finite temperature should however be computed by differentiating the free energy expression F_LDA+DMFT , which is stationary. The consequence of stationarity is that the vertex function Γ_V does not appear in the final expression for the force. More precisely, if the implementation of the force is carried out within a complete and origin-less basis set, such as the plane waves, than the force is given just by the Hellmann-Feynman Force (see Ref. [22]). Our LAPW basis set contains also the atom-centered basis functions, which generate so-called Pulley forces. In Ref. [22] this force was implemented, and it was found quite surprisingly that the computation of the force is numerically more stable than computation of the free energy formula Eq. 10. This is because it is numerically quite hard to compute the DMFT Luttinger-Ward functional Φ^DMFT , which appears in the free energy. On the other hand, the force expression depends only on its derivative δΦ^DMFT ∕δG, which is the DMFT self-energy, and can be computed very precisely by the continuous time quantum Monte Carlo method [7].

References