Home What is? Install Overview CTQMC docker MnO FeSe SrVO3 LaVO3 Cerium Sr2IrO4 Ta2NiSe5 phonon High-throughput

Docker Tutorial: Runing eDMFT in Docker

This tutorial is useful to demonstrate several new feature in eDMFT code, and to learn how to use twisted bilayer graphene (TBG) code. We show three examples, MnO (which is also covered in Tutorial 1), CrSb in magnetic state(which is not covered elsewhere) and TBG.
It is also useful to try the software without installing it locally, or to crosscheck the local installation. It only requires python with matplotlib (for plotting) and docker-desktop.

To install docker, please refer to these instructions for mac, windows, linux. The image name is haulek/edmftf, which is build for both the new silicon cpu for mac (arm64) as well as intel based cpus (amd64). The tag of the image is latest. The container is based on linux, so during installation you might want to choose to use primarily "Linux containers". The installation on Mac and linux should be very straightforward.
For installation of docker on Windows, you might want to follow the instructions here Setting Up Docker on Windows: A Step-by-Step Guide, or watch the video How To Install Docker on Windows? A Step-by-Step Guide, or, Docker Desktop for Windows 10/11 Setup and Tips.

Example 1: MnO example

Step 1: Install and Start Docker Desktop

First, install Docker Desktop locally and start the Docker application. Once Docker Desktop is running, use the search menu to look for the image by entering: haulek/edmftf or edmftf After finding the image, click on Pull to download it. The alternative is to issue in the command prompt
docker pull haulek/edmftf:latest
This action will fetch the required image to execute eDMFT in Docker. Note that Docker Desktop needs to be running in order to pull the image.

Step 2: Create a Directory for Output Files

Next, create an empty directory ( we will call it examples) somewhere on your local drive. This directory will store files generated during the Docker run. Since graphical output is not included in this Docker, we will plot results using Python on local machine (outside Docker). We will copy all relevant Python plotting scripts into this local directory to ensure accessibility outside Docker.

Step 3: Start an Interactive Docker Session

Once the image is downloaded and the examples directory is created, start an interactive Docker session by running the following command:

docker run -it -v ./examples:/root/examples haulek/edmftf /bin/bash
On windows this comman might need to be slightly modified:
docker run -it -v <local-path-windows-syntax>:/root/examples haulek/edmftf /bin/bash
If you get a lot of warnings on your computer, you might want to set export FI_PROVIDER=^psm3, which switches off psm3 warnings (when occuring).
Here is what each part of the command does: If you want to only check whether the image is working, execute
docker run -it haulek/edmftf
This will not link docker files with your operating system, hence you would not be able to see these files on your filesystem outside docker, and plot data outside docker.

The session will start an interactive shell. In this shell, navigate to the examples directory by executing:
cd ~/examples/
From this point onward, all commands to be executed inside the Docker container will be shown in blue text.

Step 4: Copy Necessary Files

Copy the crystallographic information for the two examples to the current directory by running:
cp -r /app/examples/* .
This copies two examples, MnO and CrSb, as well as useful plotting scripts to the current directory (~/examples)
For TBG example a few more plotting files are needed. If you plan to run TBG, copy also the tbg_plt files from bin directory by:
cp /app/eDMFT/bin/tbg_plt_* .

Verify that all necessary files are present by running:
ll
The output should display: 
drwxr-xr-x 3 root root    96 Jan  6 19:26 CrSb
drwxr-xr-x 3 root root    96 Jan  6 19:26 MnO
-rwxr-xr-x 1 root root  5202 Jan  6 19:26 plt_akplot.py
-rw-r--r-- 1 root root 19709 Jan  6 19:26 plt_auxiliary.py
-rwxr-xr-x 1 root root  7046 Jan  6 19:26 plt_dos.py
-rwxr-xr-x 1 root root  8865 Jan  6 19:26 plt_gs.py
-rwxr-xr-x 1 root root  1573 Jan  6 19:26 plt_info.py
-rwxr-xr-x 1 root root  6178 Jan  6 19:26 plt_makplot.py
-rwxr-xr-x 1 root root  9451 Jan  6 19:26 plt_sakplot.py
-rwxr-xr-x 1 root root  4254 Jan  6 19:26 plt_spaght.py
If you navigate to the same directory on your native computer shell, you should see the same files. For the two examples, we only have structure files in the directory, namely, MnO.cif and CrSb.mcif. The first is the standard crystallographic file for non-magnetic and the latter for magnetic material.

Step 5: Initialize the Calculation

We start with the MnO example. MnO is a charge transfer insulator in a high-spin state with localized electrons. The Mn-d electrons will be treated dynamically in the calculation. For this tutorial, we will set the Coulomb interaction parameter U to 10 eV and the exchange parameter J to 1 eV. These values are typical for transition metal oxides. They can be computed by constrained-DMFT with supercell eDMFT calculation.
To initialize the calculation, execute the following command:
cd MnO
cif2indmf.py -U 10 -J 1 -T 100 -d 'exactd' -F 10 -f -w MnO.cif
This command converts the crystallographic MnO.cif file to a format compatible with Wien2k (e.g., MnO.struct) and prepares all necessary DMFT input files.
the Options are Additional Notes on Calculation Choices: After these steps we should have the following files in MnO directory: 
-rw-r--r-- 1 root root  4207 Dec 22 21:29 MnO.cif
-rw-r--r-- 1 root root  3812 Dec 22 21:41 MnO.struct
-rw-r--r-- 1 root root 23862 Dec 22 21:41 MnO.klist_band
-rw-r--r-- 1 root root   575 Dec 22 21:41 MnO.indmf
-rw-r--r-- 1 root root  1603 Dec 22 21:41 MnO.indmfl
-rw-r--r-- 1 root root   122 Dec 22 21:41 MnO.indmfi
-rw-r--r-- 1 root root  1942 Dec 22 21:41 params.dat
-rw-r--r-- 1 root root 79144 Dec 22 21:41 cif2struct.log

Step 6: Initialize and run DFT

Initialize the DFT calculation by running:
init_lapw
Perform the DFT self-consistent calculation:
run_lapw
This step should complete in a few minutes.

Step 7: Analyzing DFT results

To solve the Kohn-Sham problem along the high-symmetry path in the first Brillouin zone, execute:
x lapw1 -band
Next, navigate to the MnO directory on your local shell (outside Docker) and plot the resulting band structure:
../plt_spaght.py MnO.output1 -y-8:8
The plot will show the band structure, like that: The plot should look like:

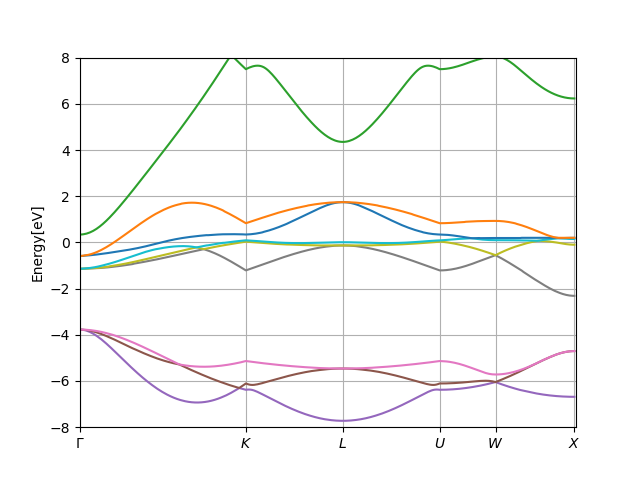
Note that black color commands in this tutorial should be executed outside docker, and blue inside docker shell. The plot shows that we have 5 bands crossing the Fermi level, which have majority Mn:3d character. The oxygen:2p bands are found between -8eV to -4eV, and Mn:4s state starts just above the Fermi level and is the wide green conduction band.

Instructions for Windows users
Under Windows the plotting through python might not yet work. First using PowerShell try to prepend the plotting command with word python, i.e.,
python ../plt_spaght.py MnO.output1 -y-8:8
If you get message that python is not installed, install it by following your windows prompt. If you just finished installing python, matplotlib library for plotting is probably not included, therefore you would need to type in PowerShell
pip install matplotlib
to install matplotlib library for python, which allows plotting. Once both python and matplotlib are in-place, you can reissue the plotting command:
python ../plt_spaght.py MnO.output1 -y-8:8
Note that all plotting commands in PowerShell require one to prepend python. We can omit that in unix based systems, because the plotting scripts appear as executables.

Step 8: Initialize DMFT run

To initialize the DMFT calculation after the DFT run, execute the following commands inside the Docker shell:
init_proj.py -a
szero.py

Step 9: Running and Monitoring the eDMFT Calculation

Configure parallel execution by writing the command for parallel execution into mpi_prefix.dat:
echo "mpirun -n 8 " > mpi_prefix.dat
Here, adjust 8 to match the number of threads your laptop supports.
Start the self-consistent eDMFT calculation:
run_dmft.py
This step may take several minutes per iteration. Monitor progress using the output files or plotting scripts. The first impurity step is done when we see the following output: 
STOP  LAPW0 END
STOP  LAPW1 END
STOP  DMFT1 END
STOP  IMPURITY_0
STOP  DMFT2 END
STOP  CORE  END
STOP  MIXER END
:ENERGY convergence: 1.0
:CHARGE convergence: 1.0
:EF     convergence: 0
:NIMP   convergence: 1
:NIMP   difference : 1
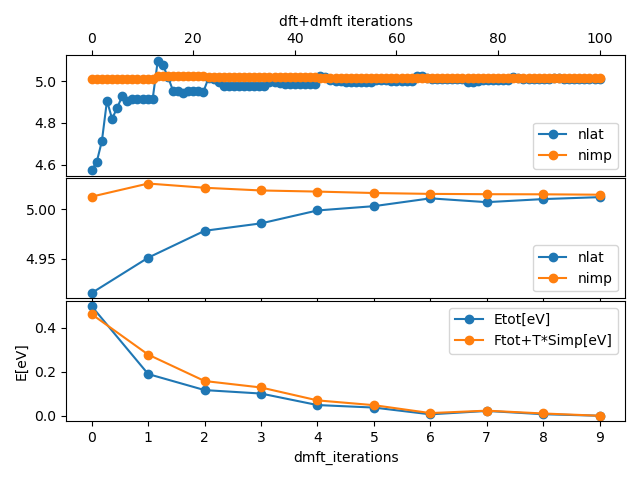
Here is a schematic plot of the calculation. Note that we first proceed on the right side down to impurity (lapw0,lapw1,dmft1,impurity) and than we go multiple times through the gray loop (around 10-times) to converge charge density (dmft2,core,mixer,lapw0,lapw1,dmft2,...). Once charge is converged, we go through the large loop and update impurity self-energy.

While the code is running (and after the first step is finished) we can start plotting the progress of the calculation. To display convergence of impurity/lattice occupancy, and total energy, we can run (outside Docker in MnO directory):
../plt_info.py

The top plot shows all DFT and DMFT steps and the Mn:5d charge as found from impurity occupancy (nimp) and from integrating charge within muffin-tin sphere in solid (nlat). The second plot shows the same two quantities, but only on converged DFT charge (and each DMFT self-energy). Namely, after impurity self-energy is recomputed, we converge DFT charge on current self-energy. The bottom plot show the total energy and total free energy of the system and its changes through iterations. It should look like:

We can also monitor how similar are impurity Greens function and lattice Greens function. We can do that by executing
../plt_gs.py -x:5 -a 6
This plots up to 5eV frequency range, and displays last 6 impurity Greens function. When the calculation is converged, the last impurity Greens function should coincide with the lattice computed Greens function. Towards the end, the plot should look like:

We see that at the beginning the current lattice Greens function and impurity Greens function do not coincide, but they get closer with each iteration (subject to MC noise).
To plot the last step only, we execute:
../plt_gs.py -x:5
and if the line and dots coincide, we reached self-consistency.

The convergence is not perfect since we use only 10 steps and only 8 processors for MC calculation. But it is good enough that we can proceed with real axis calculation.
Since we fixed the chemical potential, we need to check that the system is charge neutral. This is achieved by
grep ':DRHO' MnO.scf
The numbers should be much smaller than unity. A unit of charge here correspond to doping of 1 electron.

We can also monitor other files during calculation. For example:
If you need the second shell inside the docker to correct something, or to see files that are not exposed to native shell, you can issue: docker ps to find ID of your running docker. Thank you can execute: docker exec -it <ID> /bin/bash.

Step 10: Real Axis Calculation and Spectral Plotting

The calculation was performed on imaginary axis, and now we want to perform analytic continuation to the real axis, and display density of states and the spectral function. To do that, we execute inside Docker shell:
to_real_axis.py -y-6:6
Here -y-6:6 means that the spectral function will have frequency range from -6eV to 6eV.
This scripts execute several steps. First the maximum entropy method is run (inside maxent subdirectory), and than one DFT+eDMFT iteration is performed on the real axis (inside onreal subdirectory). We obtained density of states, the green's function on the real axis, and the momentum resolved spectral function. To display them we execute outside the docker:
cd onreal
../../plt_gs.py -x-12:12
../../plt_dos.py -x-12:12
../../plt_akplot.py
The plot of the Greens function (plt_gs.py) should produce a plot like that:

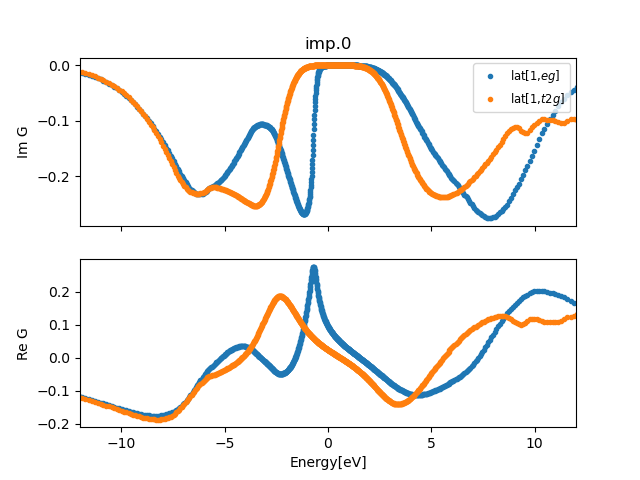
We see a clear gap of the order of 2.5eV at the Fermi level. The first valence excitation is from eg state, which strongly hybridizes with the oxygen below the Fermi level. The first conduction state is of t2g origin. Interestingly, our large Coulomb repulsion of 10eV is not clearly seen in our plot. This is because it is screened by the oxygen:p bands and Mn:4s state, so that the Hubbard bands appear much closer than they would in a corresponding Hubbard model.



The density of states displays all states, including oxygen, and we can see that less than 50% of the first excitation in the valence state is of Mn:eg character, and the rest is of oxygen:2p character. Since majority of the states just below the Fermi level are of oxygen character, this material is characterized as charge-transfer insulator, according to Zaanen-Sawatzky-Allen classification. The upper Hubbard band is majority of Mn:3d character, even though there is approximately 40% of charge that is not Mn:3d. Some is Mn:4s, and some interstitial charge.

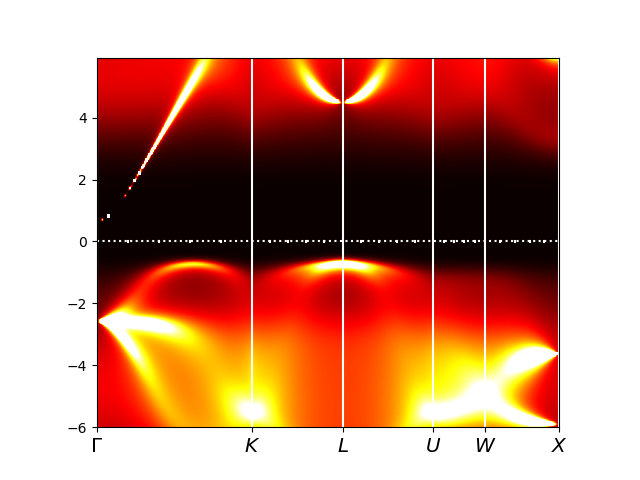
Finally, the spectral density plot (plt_akplot.py) displays the momentum resolved spectra, which has some similarity with the DFT bands, displayed earlier, but there are vast differences. The oxygen:p bands, which were mostly below -4eV, are still somewhat similar, although they move closet to EF (-3eV because of reduced level repulsion), and became broad due to hybridization with Mn:3d. The mixture of oxygen and Mn:3d is so-called Zhang-Rice singlet, which is the first occupied state (between -2eV and EF), which is all that is left from Mn:3d bands in DFT. The unoccupied Mn:4s band is not changed much, but all the Mn:3d disappeared to above 4eV, and is just a broad diffusive spectra, comprising the Hubbard band.

Example 2: CrSb altermagnet

Step 1: Initialize CrSb

Navigate to CrSb example directory:
cd ~/examples/CrSb
Currently we only have CrSb.mcif file, which describes its crystal structure and magnetic configuration. It can be displayed (for example) by VESTA, which should show:

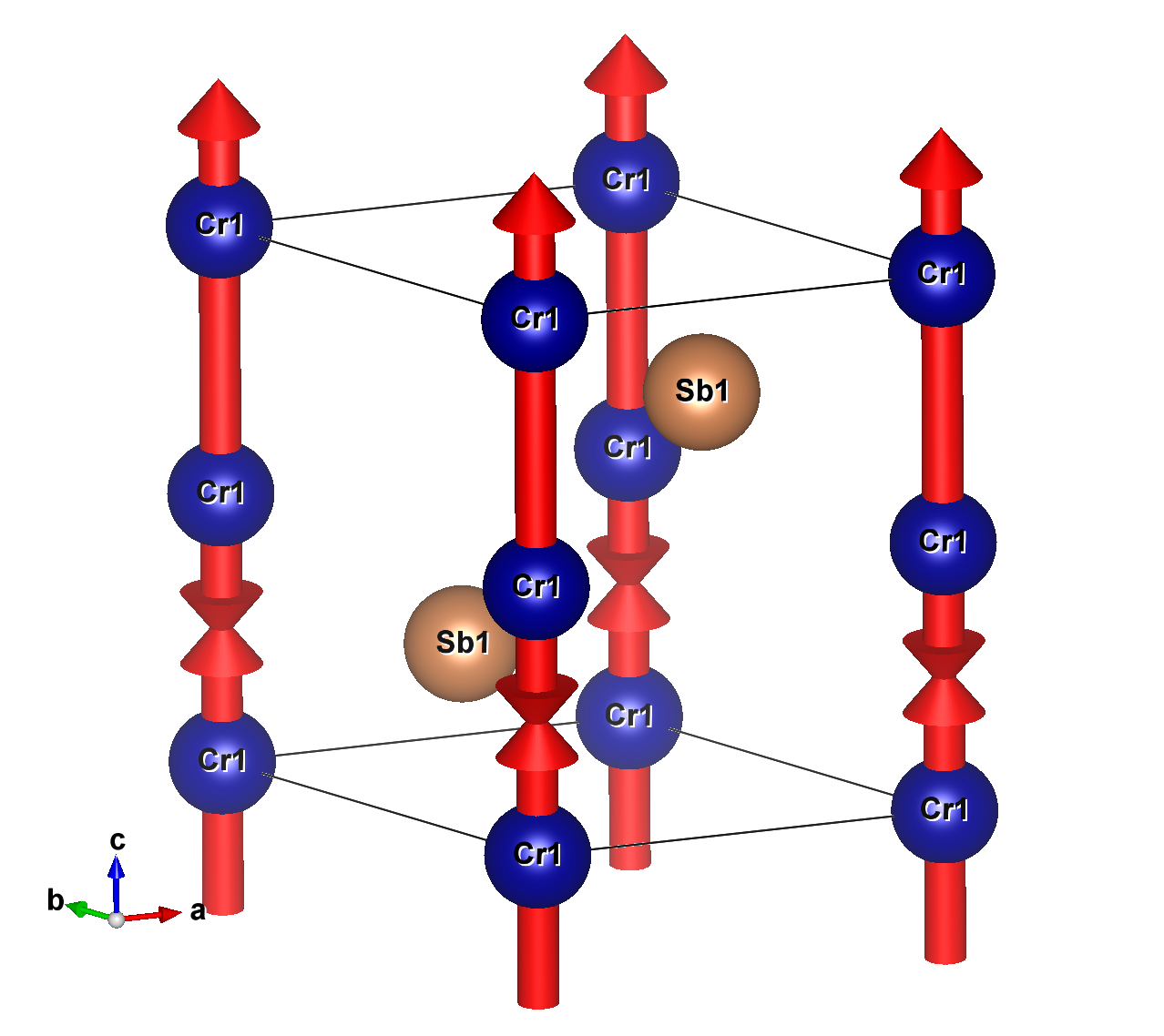
CrSb is altermagnetic (not AFM but AM) compound that crystalizes in hexagonal space group (194) with magnetic space group P63'/m'm'c (194.268) More information about this material can be found at Bilbao server. We initialize the calculation by
cif2indmf.py -m -F 10 -w CrSb.mcif
the Options are We should have the following files now: 
-rw-r--r-- 1 root root  3158 Dec 22 21:29 CrSb.mcif
-rw-r--r-- 1 root root  1898 Dec 22 22:22 CrSb.struct
-rw-r--r-- 1 root root 23783 Dec 22 22:22 CrSb.klist_band
-rw-r--r-- 1 root root  1046 Dec 22 22:22 CrSb.indmf
-rw-r--r-- 1 root root  3052 Dec 22 22:22 CrSb.indmfl
-rw-r--r-- 1 root root  3052 Dec 22 22:22 CrSb.indmfldn
-rw-r--r-- 1 root root   378 Dec 22 22:22 CrSb.indmfi
-rw-r--r-- 1 root root  1942 Dec 22 22:22 params.dat
-rw-r--r-- 1 root root 37869 Dec 22 22:22 cif2struct.log

Step 2: Initialize and run DFT

Initialize the DFT calculation:
init_lapw
Perform the DFT (non-magnetic) self-consistent calculation:
run_lapw
This step should complete in a few minutes.
Next we check the DFT band structure by executing
x lapw1 -band
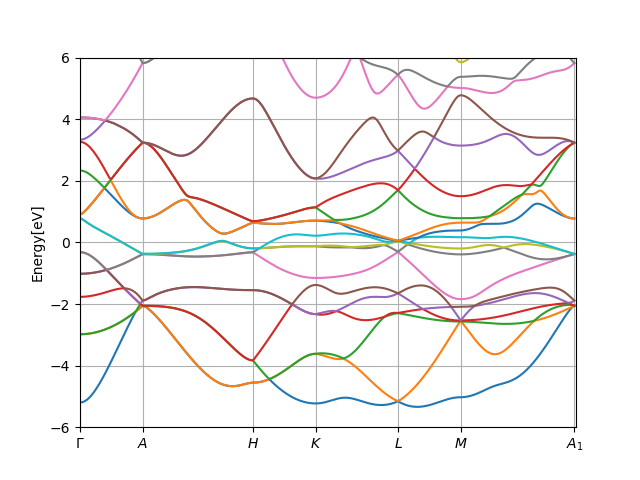
Next, navigate to the CrSb directory on your local shell (outside Docker) and plot the resulting DFT band structure:
../plt_spaght.py CrSb.output1 -y-6:6
The plot should look like:

Step 3: Initialize and run eDMFT

Next we need to compute quasi-atomi orbital on current DFT charge density, which is achieved by
init_proj.py -a
The blank self-energy is obtained by
szero.py -m
Here we added additional flag "-m", which adds some initial exchange splitting to the self-energy. This should push the calculation towards magnetic solution.
We also prepare parallel execution by
echo "mpirun -n 8 " > mpi_prefix.dat
and finally run eDMFT by
run_dmft.py
This should take approximately 40 minutes to complete 10 eDMFT steps. The metallic systems are typically slower because the perturbation order is larger. Indeed, we can check that average perturbation order in hybridization expansion Monte Carlo is 290 and maximum is 450 (check "imp.0/histogram.dat").
We can monitor the convergence with (on native shell inside CrSb directory)
../plt_info.py
which should give

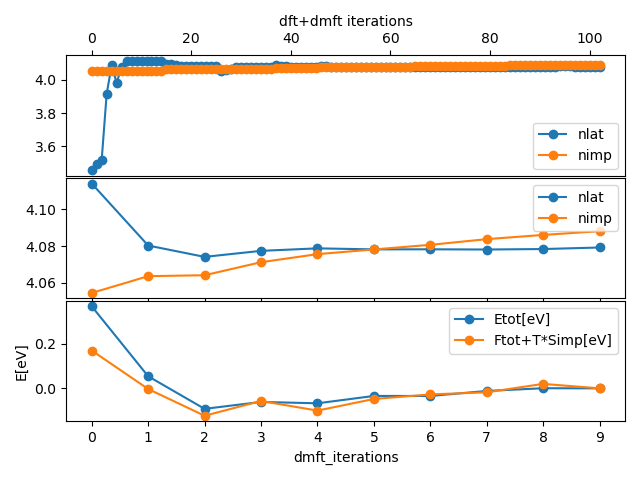
And as before, we can plot current Greens function by
../plt_gs.py -x:5
and should show

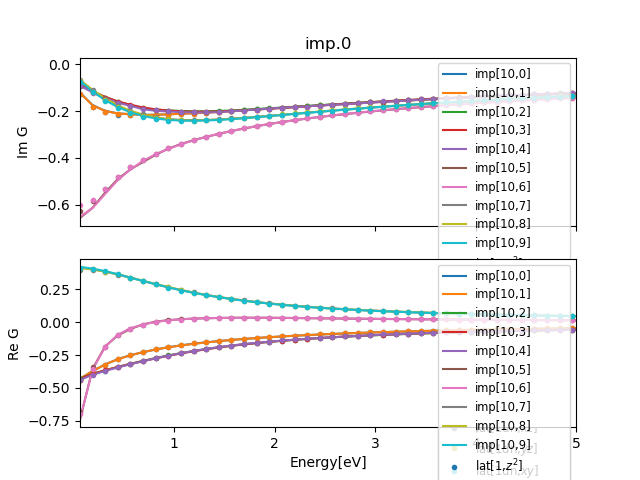
Notice that you can click on the legend to hide or replot each curve. These plots have so-called dynamic legend.

Step 4: Plot results of eDMFT on real axis

Analytic continuation and plotting spectra can be achieved by one command:
to_real_axis.py -y-6:6
Once this finishes, one can plot the green's function, density of states and the spectral function. First navigate to onreal directory on your native shell, and than execute
../../plt_gs.py -x-6:6
../../plt_dos.py -x-6:6
../../plt_akplot.py
which should give:



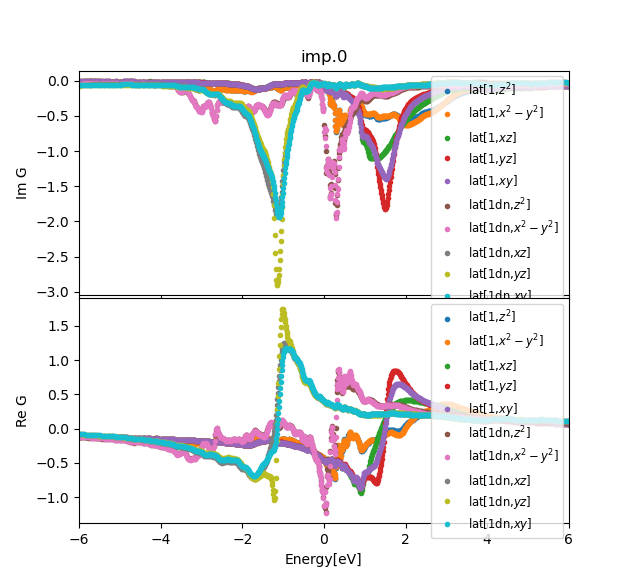
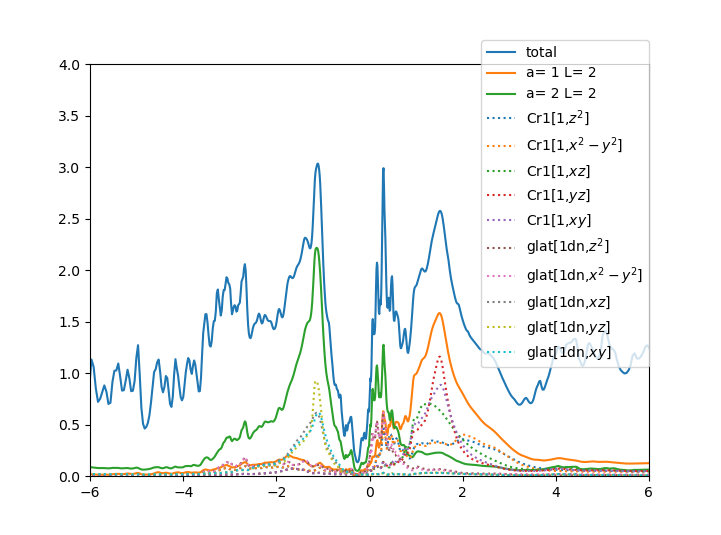
Since this is magnetic calculation the two different spin directions do not necessary have the same spectra. In conventional AFM the Kramers degeneracy is protected, but in altermagnets it is lifted at least in part of momentum space. For CrSb, this is indeed the case on xz plane, which is here achieved with the path from M to A:
../../plt_makplot.py
In most of the path the red and blue spectra coincide (Kramers degeneracy for spin-up and spin-down). In the path from M to A the degeneracy is lifted:

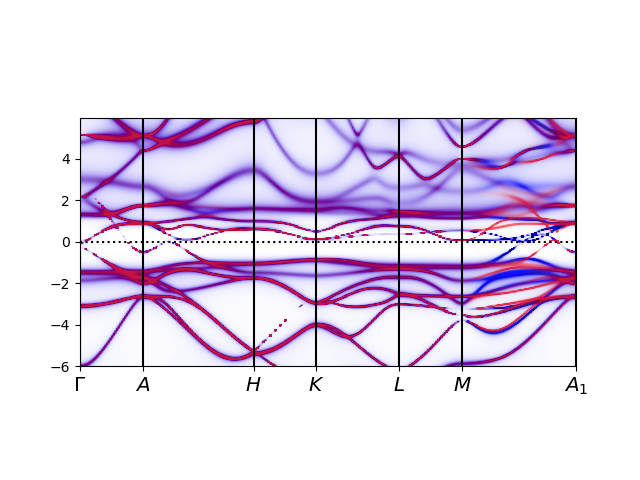
Notice that the first Brillouine zone has this form:

CrSb has lifted Kramers degeneracy in the generic point of xz (blue and green) plane, but has degeneracy in yz (orange) plane as well as xy plane and at the edge of BZ. Verify that all sections of the path in above plot, except M-A, fall on planes with Kramers degeneracy. You can produce this plot with bz.py command.

Example 3: Twisted bilayer graphene

This example is somewhat different and demonstrates the power of embedded DMFT idea, even when direct DFT is hard to perform. The basic model comes from A.H. MacDonald,'s tight binding parametrization of the twisted bilayer graphene, and the embedding DMFT idea was explained in Haule, M., Andrei, E. Y. & Haule, K.https://arxiv.org/abs/1901.09852 (2019); and results were published in Jiang, Y. et al., Nature 573, 91-95 (2019).

Here we will reproduce the calculation from the above Nature article. In the newer version of eDMFT code, there is a subdirectory called tbg, which contains all the python codes for this work. The executables are copied to your bin directory, hence they should already be in your path. For this examples, it is important that env variable PYTHONPATH is set to this bin directory, which should be in variable WIEN_DMFT_ROOT. So, check that WIEN_DMFT_ROOT is set, and that PYTHONPATH contains this directory as well.

To start, we first create new directory, say tbg, and while in that directory, we execute:
tbg_dft.py
tbg_projector.py
The first computes the tight-binding Koh-Sham like bands for twisted bilayer graphene, and the second computes the overlap between the Bloch bands and the local orbitals for eDMFT calculation. The local orbitals are defined as follows:

These four orbitals φ0(1) , φ0(2), φ0(3), φ0(4) are defined in real space. Their overlap with the Bloch-bands is computed by a real space integral/sum in tbg_projector.py. φ0(r) is a gaussian centered on AA or AB site.

All other parameters used in the calculation are available in tbg_params.py, which are written to the current directory. For example, parameter par_bs['itheta']=31 selects the angle of rotation between the two sheets of graphene. The formula for the angle for commensurate rotations is

tan(θ/2) = 1/(2√3)/( itheta + 0.5 )

and itheta is set to 31 by default, which corresponds to angle theta=1.05012 degrees. This is one of the magic angles. We will set a unit in par_bs['itheta']=50, which means that we will measure all quantities in units of 50meV. Namely, units in this example are very different than we normally deal with, hence normalizing to an appropriate unit of the order of unity is useful. All datafiles will hence contain quantities in units of 50meV.

Next we set check in tbg_params.py the following two parameters are set for plotting bands: 
par['axis']='real'    # for real axis plotting
par['plt_w']=[-2.2,2.2,300]  # for frequency range -2.2*unit,2.2*unit, 300 points, here unit=50meV
We than execute
tbg_dmft_scc.py
which produces so-called fat band plot, i.e., the color of bands now depends on projection of local orbitals φ0(1), φ0(2), φ0(3), φ0(4) to the band.

We display the fat-bands plot with:
tbg_plt_akplot.py
Note that this can not be done inside the Docker, and tbg_plt_akplot.py should be copied to the current directory, and executed outside the docker.

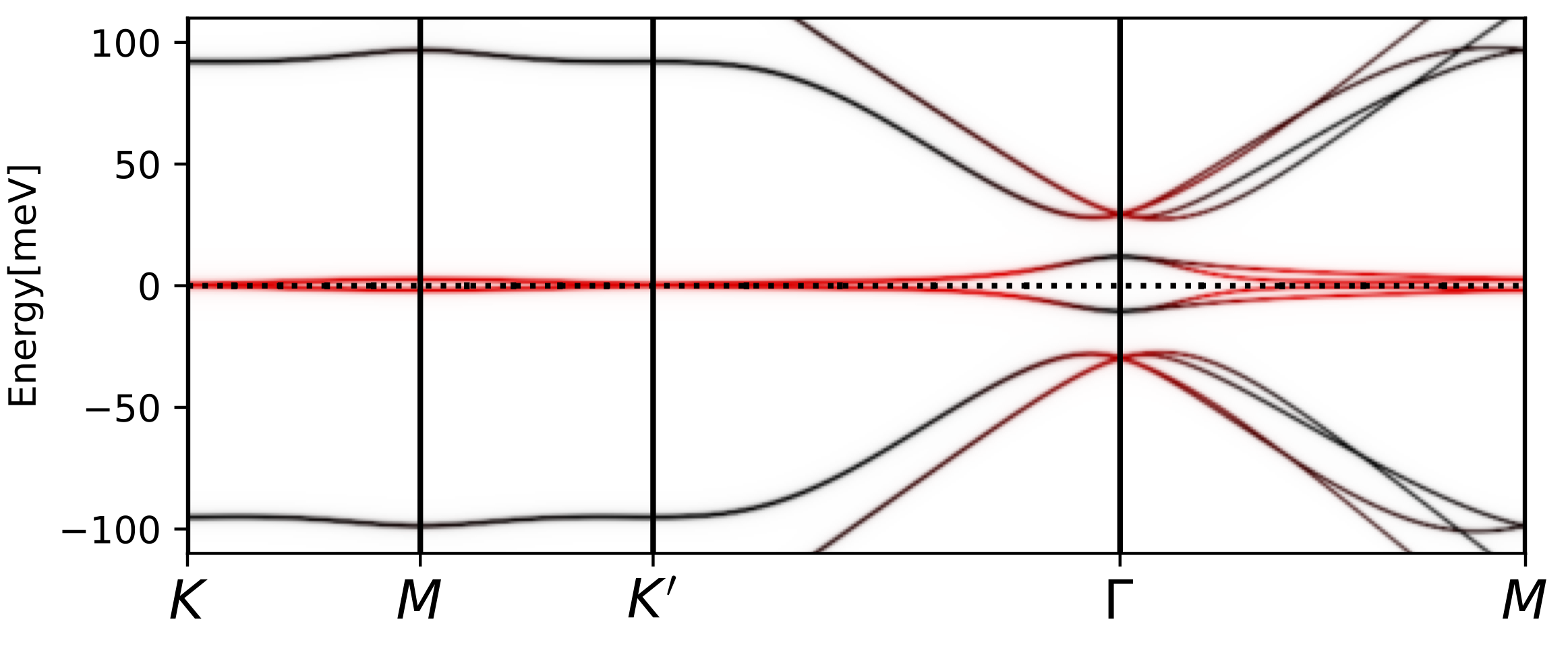
We should see a plot like above. Note that red color displays where the four local orbitals have significant overlap with bands. As is clear, the overlap is large for the four low energy bands, except at Gamma point, where the character of the bands is inverted by topology.

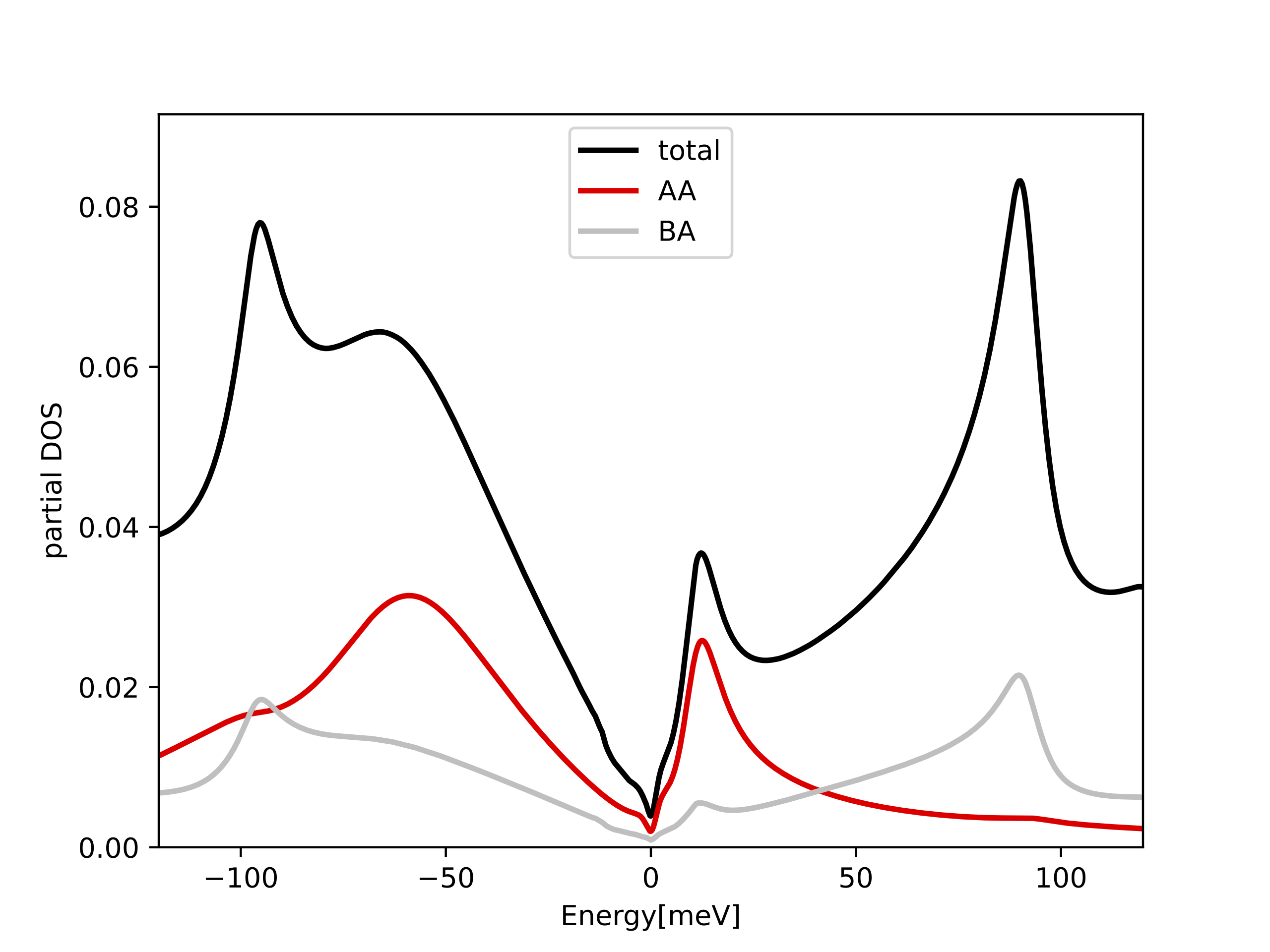
Next we plot the partial and total density of states for this Bloch band-structure. We first edit tbg_params.py and set 
par_bs['PlotBands'] = False
and than execute:
tbg_dft.py
tbg_projector.py
when calculation is done, we plot the density of states by
tbg_plt_dos.py -x-15:15
Here again the plotting should be done outside docker. The plot should look like:

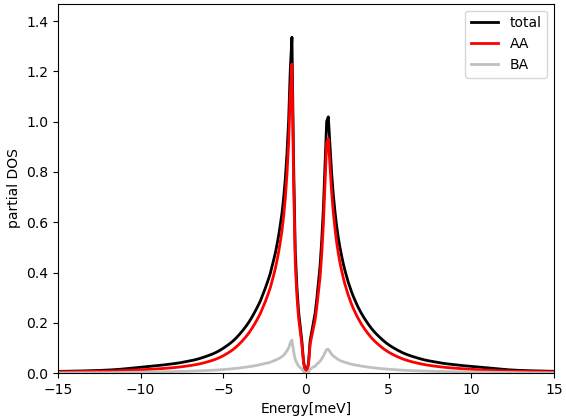
and in larger energy window:

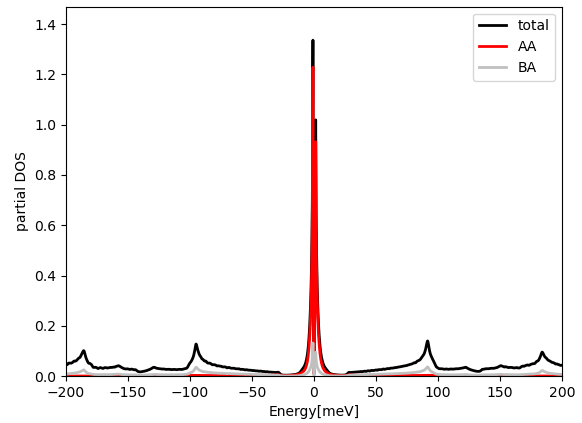
We emphasize here that the total DOS in the low energy peaks is almost entirely contained in the projected DOS to the above orbitals centered on the AA site (φ0(r)). Namely, when we compute the overlap in real space, we select a gaussian of width par_pr['optimal_r'] centered on the AA site. If we compute the overlap centered on the AB site, the overlap with these peaks is much smaller (silver curve). If we sum the two projections up, we get essentially 100% of total DOS within an energy windows of 3meV around EF. This confirms that the selected real space orbitals contain all the weight of the tight-binding model at low energy.

We can also check the hybridization of the selected orbitals with the rest of the lattice, stored in Delta.inp. The first four complex functions correspond to the local orbitals centered on the AA site, and the last four to the orbitals centered on the AB site. Of course, the hybridization of the AA-centered orbitals is small, and the hybridization of the much more extended AB-centered orbitals is several order of magnitude larger. We will therefore correlated only AA-centered orbitals. The code actually correlates both, AA and AB centered orbitals, and treats them as two independent impurity problems. But we will not run MC for the AB-centered impurity, because keeping self-energy at zero is a very good approximation. We will see warnings throughout the execution:
WARNING : did not manage to read sigma from imp.1/Sigma.inp. Creating empty self-energy which can be ignored. It says that the second impurity problem is not being run, and hence imp.1 has vanishing self-energy.

Next we change tbg_params.py for eDMFT execution. We need to set 
par['axis']='imag'           # for imaginary axis impurity solver
Nf=<number between 0 and 8>  # set Nf occupancy
The second line sets the occupancy, which can be between 0 and 8. Namely, we have 4 correlated orbitals, hence the maximum occupancy that can be achieved is 8.
Next, we execute:
tbg_dmft_scc.py
to produce empty self-energy and starting hybridization on the imaginary axis. We than set mpi_prefix.dat for parallel execution, for example,
echo "mpirun -n 8" > mpi_prefix.dat
and finally execute:
tbg_iterate.py
Note that these orbitals have very small hybridization compared to their Coulomb repulsion, yet they get quite itinerant at low energy (perturbation order is of the order of beta), hence this is difficult to handle by hybridization expansion MC, and it requires many processors to reduce MC noise. Nevertheless, up to some MC noise, we can obtain reasonable approximation even on the laptop with handful of cores. Once the 50 iterations have been completed (it might take an hour or two), we can proceed with plotting the resulting density of states and spectral functions.

We first create a new directory for analytic continuation, say maxent and average over the last few steps for better approximation to our imaginary axis self-energy
mkdir maxent
cd maxent
saverage.py -n ../imp.0/Sigma.inp.4?
maxent_run.py sig.inpx
The last command executes the maximum entropy method to get self-energy on the real axis. We obtain Sig.out. Because the scales are somewhat smaller in this calculation as opposed to most other materials, we need to adjust some parameters in maxent_params.dat. The file maxent_params.dat appears on the current directory. We set 
  
params["L"]=10
params["x0"]=0.002
And than we rerun maxent_run.py by
maxent_run.py sig.inpx
Once this is finished, we copy the resulting real-axis self-energy in place of imaginary axis self-energy, i.e.,
cp Sig.out ../imp.0/Sigma.inp_real
cd ../
and we also need to change tbg_params.py for real axis calculation: 
  
par['axis']='real'
par['Sigma']='Sigma.inp_real'
And than we compute the density of states on the real axis by:
tbg_dmft_scc.py
and display the plot by
tbg_plt_dos.py -x-200:200
The plot for charge neutral point (Nf=4) should look like:

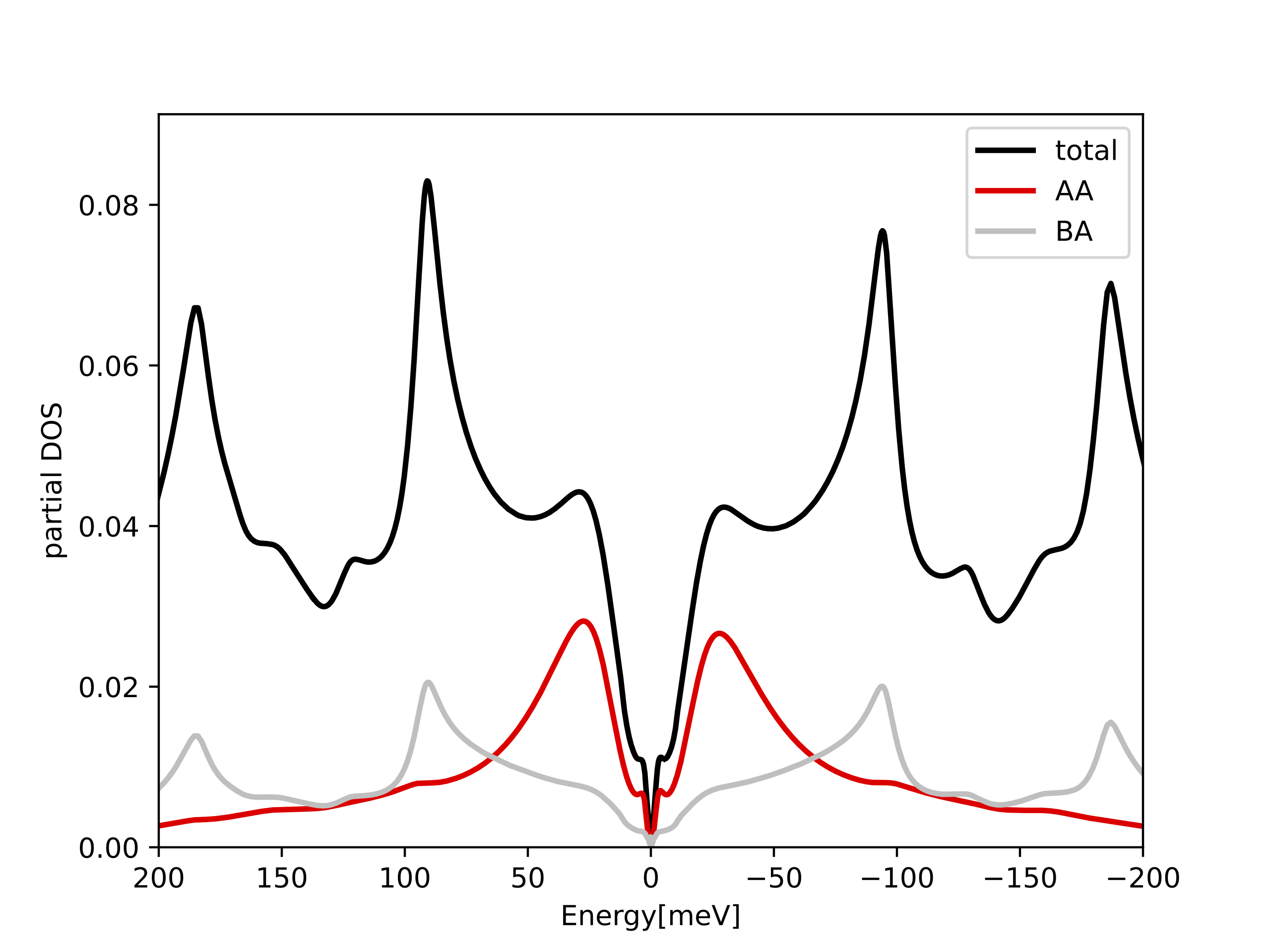
Note that the large peak at EF is transfered into the Hubbard bands, which are located around -25meV and 25meV. Their separation is thus 50meV. Naively we would expect this scale to be U. However, the U parameter which we used is 3*50meV=150meV (see the cited paper for details of estimating Coulomb U). The screened interaction is thus 50meV, and is 3 times smaller than the bare U we used. It is quite common in embedded DMFT that the Hubbard band separation is not related to Hubbard U, but rather to emergen scale, the screened U.

Next, we change tbg_params.py one more time and set: 
  
pars_bs['PlotBands']=True
And than we execute:
tbg_dmft_scc.py
tbg_plt_akplot.py -i 0.85 -b 1e-4
We should get a plot like

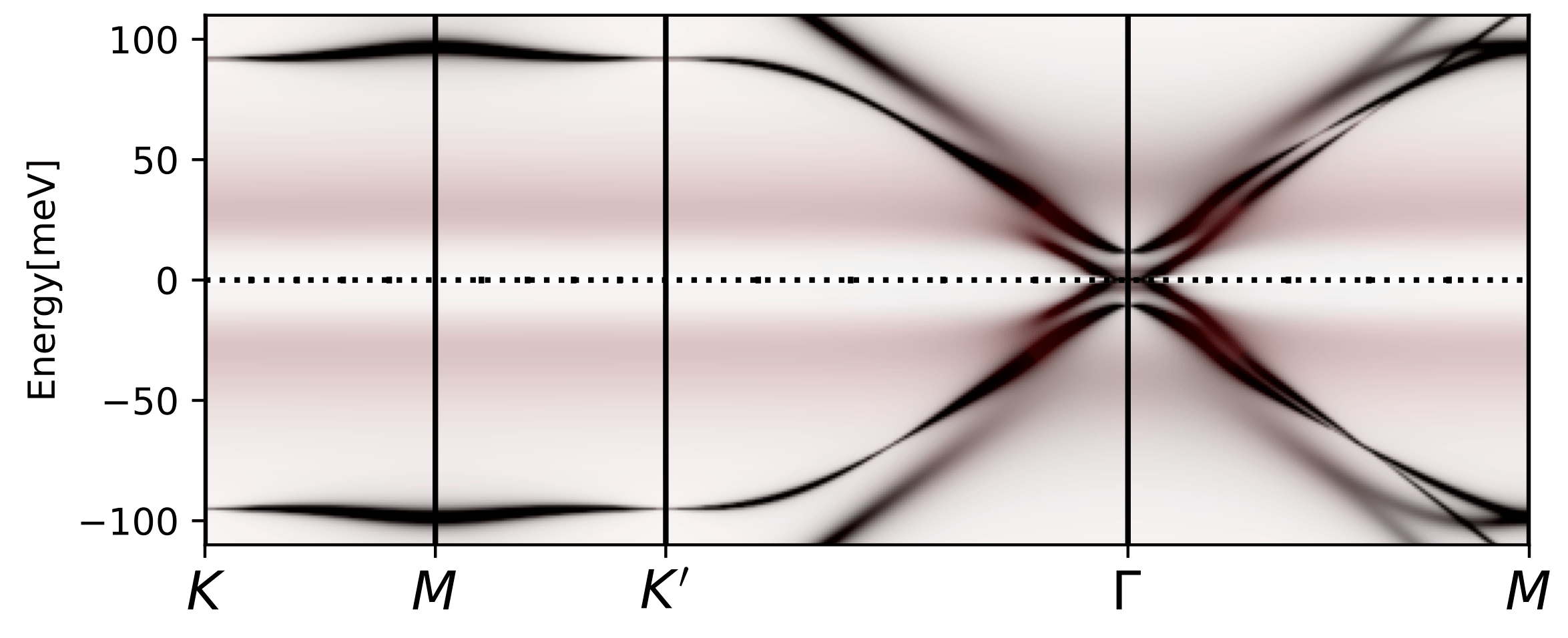
The diffuse, flat in momentum, spectral weight that has red color and is distributed between 10-50meV corresponds to the Hubbard bands we see above. The low energy states at the Gamma point appear due to non-trivial topology of the band structure, and can not be gapped out by Coulomb repulsion on the AA (or AB) site. Only breaking the symmetry can gap it out. The steep rise in the DOS above is related to these topologically protected states that are not gapped out. These states are very strongly scattered by the incoherent states, hence they do not show up in transport measurement.

If we repeat the same calculation at filling Nf=2, which has two less electrons than charge neutrality point, we get the following plots:

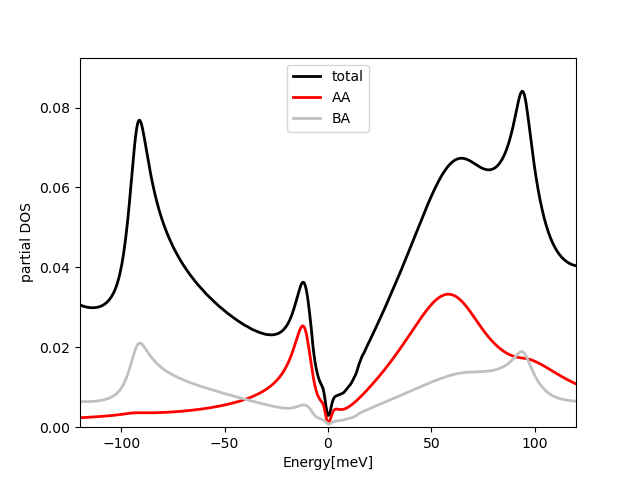
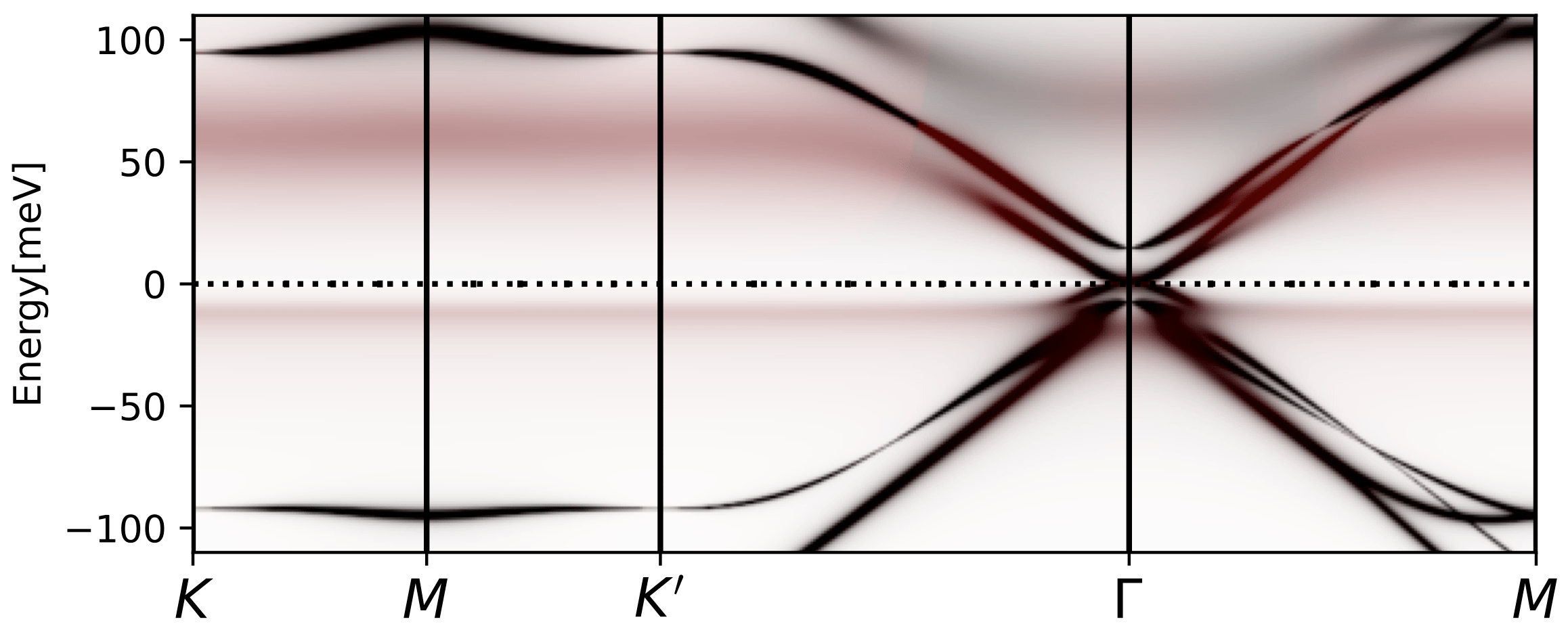
The lower Hubbard band moves closer to EF and the upper away from it, as expected. The spectral function has similar dispersion at Gamma point, which is left over from itinerant states, and it does not change with doping. But the correlated bands change a lot and they are very asymmetric.
If we change Nf to 6, we get the opposite effect, with lower Hubbard band further from EF and upper Hubbard band closer. The spectral function changes accordingly. The resulting plots are displayed below: