Home What is? Install Overview CTQMC MnO FeSe SrVO3 LaVO3 Cerium Sr2IrO4 Ta2NiSe5 phonon

Tutorial 9: High-throughput functionality

This tutorial is on the two scripts that are provided for high throughput type calculations within DFT+eDMFT. The scripts are "cif2struct.py" and "cif2indmf.py". The first converts cif (or magnetic mcif) file to proper structure file for wien2k calculation, while the latter also prepares all necessary input files for eDMFT calculation (as well as converts cif to structure file).

They require pymatgen installation. The code has been tested with pymatgen version "2023.11.12" and "2024.2.8".

The first script is cif2struct.py, which was already mentioned before. It has several options, which are available through "-h" or "--help" flag. 
Options:
  -h, --help            show this help message and exit
  -w, --writek          weather to write case.klist_band high symmetry k-path
                        (default False)
  -N NKP, --Nkp=NKP     number of k-points along the high symmetry path
  -l LOG, --log=LOG     info file
  -n, --neigh           compute neighbors and evaluate Rmt
  -m, --magnet          should produce magnetic dft struct that allows broken
                        symmetry from mcif
  -H, --hexagonal       switches off hexagonal to rhombohedral conversion
  -p NDECIMALS, --ndecimals=NDECIMALS
                        precision when determining the equivalency of atoms we
                        take nn distance with precision ndecimals. Compatible
                        with w2k nn method.
  -R NRADIUS, --nradius=NRADIUS
                        How far in AA should nearest neighbors be checked.
                        Compatible with w2k nn method.
With "-w" one can produce the k-point list through selective high-symmetry points in the BZ. These special k-points are tabulated in pymatgen, and this code just produces integer lists needed in wien2k and transformes the k-points to conventional unit cell (note that VASP and most other packages require k-points in primitive BZ).
With "-N" we can increase or reduce the number of k-points. With -l we can change the log filename, which is cif2struct.log by default, and is very useful to read.
If the cif file is magnetic mcif file, we can switch on "-m" option to produce input for magnetic calculation (no SO).
By default we convert hexagonal structures to rhombohedral as wien2k would do it later in initialization. But we don't want to change structure later, because in this case we also need to change local axis again. The "-H" switch allows one to not perform this conversion.
We can also produce nearest neighbor list with "-n" and correctly set RMT radius in structure file. But this neighbors list is crucial for the second script, namely, 
 cif2indmf.py -w case.cif
which produces a complete set of all input files for dmft calculation, which are a good guess for a best set of parameters.
The script takes many optional parameters: 
Options:
  -h, --help            show this help message and exit
  -w, --writek          weather to write case.klist_band high symmetry k-path
                        (default False)
  -s, --so              is this with spin-orbit or not (default False)
  -r, --real            real axis sets matsubara to 0 in indmffile (default
                        False)
  -f, --fix             fix the chemical potential for Mott insulators
                        (default False)
  -N NKP, --Nkp=NKP     number of k-points along the high symmetry path
                        (default 300)
  -l LOG, --log=LOG     info file (default cif2struct.log)
  -c COR, --cor=COR     which atom types are correlated. all or 3,4 or 3-5 or
                        6-7 (default all)
  -d DC, --dc=DC        The type of double-counting: exact, exacty, exactd,
                        nominal (default exacty)
  -U COULOMBU, --U=COULOMBU
                        Coulomb U if we want to set it through input (default
                        None, set inside for each type)
  -J COULOMBJ, --J=COULOMBJ
                        Coulomb J if we want to set it through input (default
                        None, set inside for each type)
  -b BETA, --beta=BETA  inverse temperature (default 50/eV->232K)
  -M QMC_M, --QMC_M=QMC_M
                        Number of MC steps per core (default = 5M)
  -q QSPLIT, --qsplit=QSPLIT
                        qsplit (default = 2)
  -m, --magnet          should produce magnetic dft struct that allows broken
                        symmetry from mcif
  -H, --hexagonal       switches off hexagonal to rhombohedral conversion
  -p NDECIMALS, --ndecimals=NDECIMALS
                        precision when determining the equivalency of atoms we
                        take nn distance with precision ndecimals. Compatible
                        with w2k nn method.
  -R NRADIUS, --nradius=NRADIUS
                        How far in AA should nearest neighbors be checked.
                        Compatible with w2k nn method.
Here '-w', '-s', '-r', '-f' don't take any arguments, just set that particular option to true. For example, '-s' sets spin-orbit to True. The rest of the options require an argument. For example '-c' takes the set of atoms to be treated as correlated. One can specify to correlate 3d,4d, or 5d ions, which is set by values 3, 4, or 5. We can correlated all at the same time with 3,4,5 or 3-5. For rare earths we give number 6 and for actinides 7. By default all those should be correlated, hence -c 3-7 is default. Only a set of elements in each row are actually treated as correlated, namely, 
{3:["V","Cr","Mn","Fe","Co","Ni","Cu"],
 4:["Nb","Mo","Tc","Ru","Rh","Pd"],
 5:["Ta","W","Re","Os","Ir","Pt"],
 6:["Ce","Pr","Nd","Pm","Sm","Eu","Gd","Tb","Dy","Ho","Er","Tm","Yb","Lu"],
 7:["Th","Pa","U","Np","Pu","Am","Cm","Bk","Cf","Es","Fm","Md","No","Lr"]
}
By default Coulomb U and J are set to the following values 
Us={3: 10., 4: 8.0, 5: 7.0, 6: 6.0, 7: 6.0}
Js={3: 0.8, 4: 0.8, 5: 0.8, 6: 0.7, 7: 0.7}
For now, qsplit=2 by default, and can be set to some other number, but must be equal for all atoms, which is probably not optimal. For lanthanides and actinides qsplit should probably be better to be 1, and for 5d 13, but in both cases we would than need spin-orbit, which is off by default. To refresh our memory, qsplit means the following choice of orbitals 
     0  average GF, non-correlated
     1  |j,mj> basis, no symmetry, except time reversal (-jz=jz)
    -1  |j,mj> basis, no symmetry, not even time reversal (-jz=jz)
     2  real harmonics basis, no symmetry, except spin (up=dn)
    -2  real harmonics basis, no symmetry, not even spin (up=dn)
     3  t2g orbitals 
    -3  eg orbitals
     4  |j,mj>, only l-1/2 and l+1/2
     5  axial symmetry in real harmonics
     6  hexagonal symmetry in real harmonics
     7  cubic symmetry in real harmonics
     8  axial symmetry in real harmonics, up different than down
     9  hexagonal symmetry in real harmonics, up different than down
    10  cubic symmetry in real harmonics, up different then down
    11  |j,mj> basis, non-zero off diagonal elements
    12  real harmonics, non-zero off diagonal elements
    13  J_eff=1/2 basis for 5d ions, non-magnetic with symmetry
    14  J_eff=1/2 basis for 5d ions, no symmetry


The harderst algorithm in this script is choosing the best local coordinate axis on all correlated atoms, so that the hybridization function has minimal off-diagonal components. For that purpose, the script includes localaxes.py script, which tries to guess the best polyhedra surrounding the correlated atom, and from the polyhedra it tries to determine the best local axis. It implements cube(8), octahedra(6), tetrahedra(4), square-piramid(5), cuboctahedron (12), truncated tetrahedron (12), peak-of-tetrahedron(3), peak-of-square-piramid(4), peak-of-hexagonal-piramid(6), trigonal prism(6), planar quadrilateral (4). In the bracket with quote the number of neighbors needed for each polyhedra.

The script cif2indmf.py will produce case.struct, case.indmf, case.indmfl, case.indmfi, params.dat, and with "-w" flag also case.klist_band. Information is written to cif2struct.log. Three things are still needed for dmft run, namely, All these values can be obtained from converged dft run, hence the third script 
 init_proj.py -a
should be run after dft run is complete. It will write real space projector to projectorw.dat. Next, it will check the band range written in case.indmf in eV around the Fermi level, and convert this number to integer band range obtained from case.energy files. Finally, it will check the dft density matrix and guess the best density nf0 for dmft double-counting, so that the starting point in double-counting is excellent. Even when we use exact double counting, we start with first guess that is proportional to this nf0 value, because we don't have impurity occupancy yet. Finally, after init_proj.py has been run, we need to call 
  
 szero.py
to produce a good guess for self-energy (best s_oo and Edc). The complete list of commands for high-throughput calculation could thus be 
  
  $WIEN_DMFT_ROOT/cif2indmf.py -w case.cif >& nohup_init.dat
  echo "mpirun -n $NSLOTS" > mpi_prefix.dat
  echo "mpirun -n $NSLOTS" > mpi_prefix.dat2
  $WIENROOT/init_lapw -b -red 0 -vxc 5 -ecut -7.0  -numk 2000 >> nohup_init.dat
  $WIEN_DMFT_ROOT/run_dft.py >> nohup_dft.dat
  $WIEN_DMFT_ROOT/init_proj.py  -a >> nohup_init.dat
  $WIEN_DMFT_ROOT/szero.py >> nohup_init.dat
  $WIEN_DMFT_ROOT/run_dmft.py >& nohup_dmft.dat
Of course one could use less k-points to converg dft, and later increase the number of k-points for dmft. But these details can be easily added. One should also check how off diagonal is the hybridization, by running one dmft1 step with qsplit=12. Namely, qsplit=12 will produce all off-diagonal hybridizations, which should be checked to be small. If not, one could possibly run 
  
$WIEN_DMFT_ROOT/findRot.py
to diagonalize hybridization on dft level before executing dmft. More about this below in the case of RuO2.

Finally, we need to use a uniform choice of parameters for all calculations. In the following we will select 
U=10eV
J=0.8eV
DCs='exact'
qsplit=2
CoulombF='Ising'
This works quite well for 3d correlated compounds which are strongly correlated. CoulombF='Full' is better, but is expensive. For metals, like Fe superconductors, U should be somewhat reduced. exact is a combination of exacty and exactd double-counting. The first is a combination of yukawa and dielectric screening that gives prescribed U and J, while the latter is purely dielectric screening. While exacty is expected to be best in many materials, it seems to be too short ranged in late TMO's, which require more dielectric type screening. As a result exact is a compromise that interpolated between exacty in early TMOs and exactd in later TMOs. With this in mind, we rerun a few compounds discussed in previous tutorials, and we will next present the results, so that user can check if the code works correctly.

SrVO3

We rerun SrVO3 with these default parameter. Notice that before we correlated only t2g orbitals and used smaller U=8eV. Now we correlate both the t2g and eg orbitals and with increased U=10eV, we produce similar spectra and similar occupancies. For example, the t2g only occupancy was before n_{t2g}=1.45, while the new calculation gives n_{t2g}=1.522 and n_{eg}=0.715. The total 3d occupancy is much bigger n_{3d}=2.24, but this is because we now count both the eg and t2g electrons. The converged results in info.file is 
    mu          Vdc            Etot     Ftot+T*Simp     Ftot+T*Simp       n_latt        n_imp      Eimp[0]     Eimp[-1] 
8.661942    15.551639    -8710.159608    -8710.165781    -8710.158820     2.240679     2.237563    -0.085963    -1.448770
Here is the plot of density of states and the Green's function for both t2g, eg, and oxygen bands.
These are similar than before, but correlations are now somewhat weaker. The mass enhancement is now only around m*/m~2 as compared to m*/m~2.5 in t2g only calculation. This is close, but if we wanted to get a better agreement with previous t2g only calculation, we would need to further reduce U in previous calculation. We notice however that the calculations are much harder to converge now, because the typical perturbation order is now around order 450 (extending beyond 500), while in t2g only calculation, the typical order was 170 (extending to 230). Finally, we show the hybridization function for t2g orbital:
This is almost identical to previous t2g only calculation.

LaVO3

In one of the previous tutorials we have performed t2g-only calculation for LaVO3, which it turned out to be Mott insulating material with t2g occupancy close to 2, and Mott gap close to, but smaller than 2eV. In this tutorial we correlated all 3d orbitals, and automatically select the best local axis. You can check that case.indmfl files has local rotation equivalent to the one we produced in previous tutorial. The self-consistent calculation with all 5d orbitals and larger U=10eV produces similar results. However, there are also difference. First we point out that the Mott gap can be numerically stabilized with fixing the chemical potential. We thus change the flag in params.dat file to 
  
recomputeEF         =0
and than check in dmft_info.out or case.outputdmf2 file that 
rho-rho_expected ~ 0
is close to zero. If there is a gap, this number will be an integer, and we must ensure it is not +1 or -1, but close to zero. The converged values in info.iterate are: 
       mu          Vdc            Etot     Ftot+T*Simp     Ftot+T*Simp       n_latt        n_imp      Eimp[0]     Eimp[-1] 
10.803055    18.468704   -77383.390671   -77383.399318   -77383.389914     2.540813     2.543642     0.025545    -1.150281
Total occupancy for eg and t2g is 2.54 electrons. We can check what is partial occupancy in imp.0/Gf.out in the first line mom lists partial occupnacies of impurity. We got the following occupancies 
      z^2                 x^2-y^2           xz                 yz                xy
mom=[0.2345946764349459,0.2332270335931207,0.7098984906471872,0.6736290320800302,0.6922923990033716,]
hence t2g occupancy is n_{t2g}=2.08, which is extremely close to previous t2g only calculation with occupancy of n_{t2g}=2.1. The local density of states is plotted below:
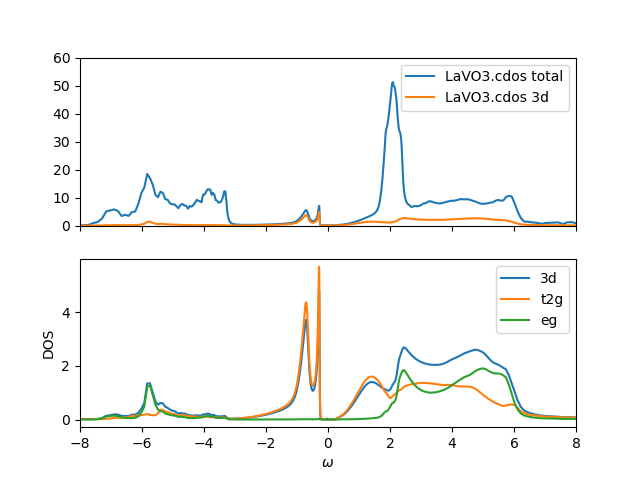It shows a small gap, and the lower Hubbard band split into Slatter peak (first peak in the valence band) and more broad reminder of the Hubbard band. This signals that the Mott gap is somewhat closer to the Mott transition (but above), hence Slater peak is very pronounced. The fact that we are close to the Mott transition was observed also numerically, as convergence is much more challenging in this settings. We notice that the eg-states have shifted slightly upward, similar as in SrVO3. This is not surprising, as correlations should remove such orbitals that are in empty orbital regime from the Fermi level. Finally, to check the size of the Mott gap we display the spectral function. We notice that the size of the gap is very comparable to what we have seen before (close to 2eV, but somewhat smaller than 2eV). We clearly see the splitting in the lower Hubbard band into Slater peak and the rest. More importantly, the conduction band is very different now. Before the conduction band started with eg states, while now it starts with La-f states.
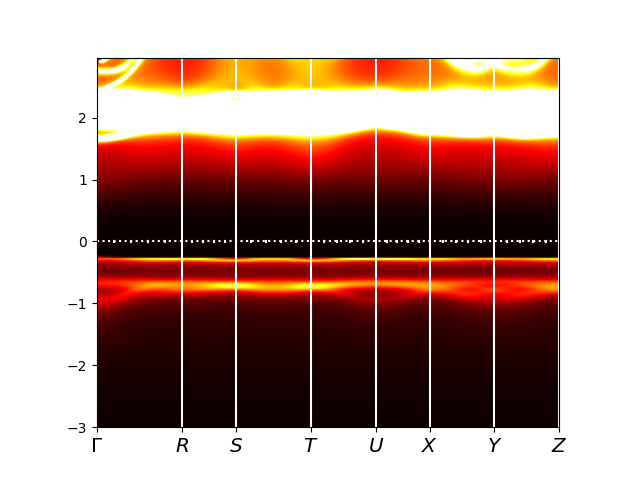Since La-f states are not treated as correlated, they might be misplaced, and it is an interesting question if more precise calculation with correlations on La-f states would increase the gap size or not.

FeSe

Finally, we also recompute the properties of FeSe with similar input parameters. If we choose U=8eV and J=0.8eV with DCs=exact, we get relaxed structure with z parameter around 0.3, and occupancy very close to 6 (nd=6.07). This parameters predict very strong correlations, a bit more than experiment shows.
When U=5eV and J=0.8eV with DCs=exact, we get a relaxes structure with z=0.281 and occupancy nd=6.26, which is in a reasonable agreement with experiment. We want to point out that occupancy could be reduced by choosing DCs=exacty, which would increase correlation strength and increase z. On the other hand, choosing DCs=exactd would do the opposite, decrease the occupancy and decrease correlations and structural parameter z. Increase of Hund's coupling has similar effect in decreasing occupancy and increasing correlation strengt. Here is the table that demonstrates the sensitivity of the results with these parameters.
U=5eV J=0.7eV J=0.8eV
DCs='exact' z=0.270, nd=6.32 z=0.281, nd=6.26
DCs='exacty' z=0.300, nd=6.02 z=0.306, nd=5.95

Notice that J and DCs are even more crucial parameters than U in this case. This is because FeSe is at the verge of selective Mott differentiation, and therefore this strong sensitivity with small variation of parameters.

RuO2 as Altermagnet

In this section we will demonstrate how to run eDMFT code for magnetic materials, in this case altermagnet RuO2. This run will be done without SO coupling, because this is the best way to distinguish between altermagnets and other antiferromagnets that have SO induced splitting of bands.

We start by downloading magnetic cif file from Bilbao Crystallographic Server (RuO2 mcif appears under number 0.607). For the purpose of this exercise we will call it 0_607_RuO2.mcif.
First we will generate all eDMFT input files with cif2indmf.py script. This script takes many options, which are listed with "-h" or "--help" option: 
Options:
  -h, --help            show this help message and exit
  -w, --writek          weather to write case.klist_band high symmetry k-path
                        (default False)
  -s, --so              is this with spin-orbit or not (default False)
  -r, --real            real axis sets matsubara to 0 in indmffile (default
                        False)
  -f, --fix             fix the chemical potential for Mott insulators
                        (default False)
  -N NKP, --Nkp=NKP     number of k-points along the high symmetry path
                        (default 300)
  -l LOG, --log=LOG     info file (default cif2struct.log)
  -c COR, --cor=COR     which atom types are correlated. all or 3,4 or 3-5 or
                        6-7 (default all)
  -d DC, --dc=DC        The type of double-counting: exact, exacty, exactd,
                        nominal (default exacty)
  -U COULOMBU, --U=COULOMBU
                        Coulomb U if we want to set it through input (default
                        None, set inside for each type)
  -J COULOMBJ, --J=COULOMBJ
                        Coulomb J if we want to set it through input (default
                        None, set inside for each type)
  -b BETA, --beta=BETA  inverse temperature (default 50/eV->232K)
  -M QMC_M, --QMC_M=QMC_M
                        Number of MC steps per core (default = 5M)
  -q QSPLIT, --qsplit=QSPLIT
                        qsplit (default = 2)
  -m, --magnet          should produce magnetic dft struct that allows broken
                        symmetry from mcif
  -H, --hexagonal       switches off hexagonal to rhombohedral conversion
  -p NDECIMALS, --ndecimals=NDECIMALS
                        precision when determining the equivalency of atoms we
                        take nn distance with precision ndecimals. Compatible
                        with w2k nn method.
  -R NRADIUS, --nradius=NRADIUS
                        How far in AA should nearest neighbors be checked.
                        Compatible with w2k nn method.

We will execute: 
cif2indmf.py -w -m -U 6.0 0_607_RuO2.mcif
in which "-m" option allows to generate all magnetic input files, "-w" creates high symmetry k-path, and "-U" reduced Coulomb U from default 8eV for 4d's to 6eV, because RuO2 is metallic. This should generate 
0_607_RuO2.struct
0_607_RuO2.indmfi
0_607_RuO2.indmfl
0_607_RuO2.indmfldn
0_607_RuO2.klist_band
params.dat
cif2struct.log
The structure file contains two inequivalent Ru atoms in P4_2/mnm space group. Also the oxygen atoms are split into O1 and O2.
It is very useful to read cif2struct.log, which explains the algorithm of generating all these files. First it prints the structure read from cif file: 
structure directly from given input cif file
---------------------------------------------
ca= 4.492 cb= 4.492 cc= 3.1061 calpha= 90.0 cbeta= 90.0 cgamma= 90.0
sgname= P  4_2/m  n  m sgnum= 136 ssetting= None
  1 Ru       0.000000, 0.000000, 0.000000
  2 O        0.305580, 0.305580, 0.000000
next it shows conventional unit cell, which is needed for Wien2k structure file (notice that some atom positions that appear in conventional but not primitive cell are remove later in the cif2struct.py algorithm): 
Full Formula (Ru2 O4)
Reduced Formula: RuO2
abc   :   4.492000   4.492000   3.106100
angles:  90.000000  90.000000  90.000000
pbc   :       True       True       True
Sites (6)
  #  SP          a        b    c    magmom
---  ----  -------  -------  ---  --------
  0  Ru    0        0        0        0.05
  1  Ru    0.5      0.5      0.5     -0.05
  2  O     0.30558  0.30558  0        0
  3  O     0.80558  0.19442  0.5      0
  4  O     0.19442  0.80558  0.5      0
  5  O     0.69442  0.69442  0        0
Next it prints all 16 symmetry operations of this magnetic system: 
Number of symmetry operations available= 16
magnetic cif= True
0 : Time=1 I
 1 0 0 0.00000000
 0 1 0 0.00000000
 0 0 1 0.00000000
1 : Time=1 R
 1 0 0 0.50000000
 0-1 0 0.50000000
 0 0-1 0.50000000
2 : Time=1 R
-1 0 0 0.50000000
 0 1 0 0.50000000
 0 0-1 0.50000000
3 : Time=1 R
-1 0 0 0.00000000
 0-1 0 0.00000000
 0 0 1 0.00000000
4 : Time=1 P
-1 0 0 0.00000000
 0-1 0 0.00000000
 0 0-1 0.00000000
5 : Time=1 R
-1 0 0 0.50000000
 0 1 0 0.50000000
 0 0 1 0.50000000
6 : Time=1 R
 1 0 0 0.50000000
 0-1 0 0.50000000
 0 0 1 0.50000000
7 : Time=1 R
 1 0 0 0.00000000
 0 1 0 0.00000000
 0 0-1 0.00000000
8 : Time=-1 R
 0-1 0 0.50000000
 1 0 0 0.50000000
 0 0 1 0.50000000
9 : Time=-1 R
 0 1 0 0.50000000
-1 0 0 0.50000000
 0 0 1 0.50000000
10 : Time=-1 R
 0 1 0 0.00000000
 1 0 0 0.00000000
 0 0-1 0.00000000
11 : Time=-1 R
 0-1 0 0.00000000
-1 0 0 0.00000000
 0 0-1 0.00000000
12 : Time=-1 R
 0 1 0 0.50000000
-1 0 0 0.50000000
 0 0-1 0.50000000
13 : Time=-1 R
 0-1 0 0.50000000
 1 0 0 0.50000000
 0 0-1 0.50000000
14 : Time=-1 R
 0-1 0 0.00000000
-1 0 0 0.00000000
 0 0 1 0.00000000
15 : Time=-1 R
 0 1 0 0.00000000
 1 0 0 0.00000000
 0 0 1 0.00000000
Here the notation is like in w2k structure file, i.e., 3x3 rotation with the last column real space translation. The time reversal (which flips the spin) is denoted by Time=+1 or Time=-1. The name R,P,I designates P for inversion, I for identity, and R for any other operation.

Next few lines show how symmetry operations split the magnetic symmetry operations to those that are present for spin-up (or spin-down) only calculation. If operation flips spins, it should be removed in spin-up calculation only. If it preserves the spin, it is kept. 
Ru[0] [0. 0. 0.] M[0]= [0.   0.   0.05]
Ru[1] [0.5 0.5 0.5] M[1]= [ 0.    0.   -0.05]
Group[1] applied to r[1]= [0.5 0.5 0.5] and M[1]= [0.0, 0.0, -0.05]  gives r[0]= [0. 0. 0.]  and M[0]= [0.0, 0.0, 0.05]
Molap= -1.0
Since moments are different ig= 1 should be removed flipped= {1: 0}
Group[2] applied to r[1]= [0.5 0.5 0.5] and M[1]= [0.0, 0.0, -0.05]  gives r[0]= [0. 0. 0.]  and M[0]= [0.0, 0.0, 0.05]
Molap= -1.0
Since moments are different ig= 2 should be removed flipped= {1: 0}
Group[5] applied to r[1]= [0.5 0.5 0.5] and M[1]= [0.0, 0.0, -0.05]  gives r[0]= [0. 0. 0.]  and M[0]= [0.0, 0.0, 0.05]
Molap= -1.0
Since moments are different ig= 5 should be removed flipped= {1: 0}
Group[6] applied to r[1]= [0.5 0.5 0.5] and M[1]= [0.0, 0.0, -0.05]  gives r[0]= [0. 0. 0.]  and M[0]= [0.0, 0.0, 0.05]
Molap= -1.0
Since moments are different ig= 6 should be removed flipped= {1: 0}
Group[8] applied to r[1]= [0.5 0.5 0.5] and M[1]= [0.0, 0.0, -0.05]  gives r[0]= [0. 0. 0.]  and M[0]= [0.0, 0.0, 0.05]
Molap= -1.0
Since moments are different ig= 8 should be removed flipped= {1: 0}
Group[9] applied to r[1]= [0.5 0.5 0.5] and M[1]= [0.0, 0.0, -0.05]  gives r[0]= [0. 0. 0.]  and M[0]= [0.0, 0.0, 0.05]
Molap= -1.0
Since moments are different ig= 9 should be removed flipped= {1: 0}
Group[12] applied to r[1]= [0.5 0.5 0.5] and M[1]= [0.0, 0.0, -0.05]  gives r[0]= [0. 0. 0.]  and M[0]= [0.0, 0.0, 0.05]
Molap= -1.0
Since moments are different ig= 12 should be removed flipped= {1: 0}
Group[13] applied to r[1]= [0.5 0.5 0.5] and M[1]= [0.0, 0.0, -0.05]  gives r[0]= [0. 0. 0.]  and M[0]= [0.0, 0.0, 0.05]
Molap= -1.0
Since moments are different ig= 13 should be removed flipped= {1: 0}
Starting anew with ii=1 grp= [[0], [1]]
groups for magnetic atoms= [[[0], [1]]]
indx_by_element {'Ru': [0, 1], 'O': [2, 3, 4, 5]}
starting with groups for magnetic atoms= [[[0], [1]], [[2, 3, 4, 5]]]
Here "Molap" means the overlap between original spin and the spin after the symmetry operation. If the spin is preserved, "Molap" is 1.0 and if it is flipped, is -1.0. Since many materials have canted magnetic moments we allow abs(Molap) to be less than unity. As long as it is bigger than 0.75, we consider spin to be parallel or antiparallel.
We apply all symmetry operations, and see that operation [1,2,5,6,8,9,12,13] transform Ru[1] to Ru[0], and also flip the spin (as they should), while the rest of the operations [0,3,4,7,10,11,14,15] don't flip spins, and they do not mix Ru[0] with Ru[1] with opposite spin, hence are preserved in our calculation.

Next we produce a list of all magnetic atoms that form equivalent group. We call that "groups for magnetic atoms", which is "[[[0],[1]]]". It means that atom 0 and 1 are different. If the list is "[[[0,1]]]" they would be considered equivalent. The non-magnetic atoms are first considered to be equivalent if they correspond to the same element. Since we only have oxygens at position 2,3,4,5, they are all considered equivalent for now, i.e., [2,3,4,5]. "indx_by_element" also shows which elements have which successive number in the structure.

Next we print for each atom which symmetry operations transforms ups into down spins. Here Ru[1] is transformed into Ru[0] and the following symmetry operations flip the spin" 
atoms which are flipped of each other:
1->0
    T=1
    R= 1, 0, 0
       0,-1, 0
       0, 0,-1
    T=1
    R=-1, 0, 0
       0, 1, 0
       0, 0,-1
    T=1
    R=-1, 0, 0
       0, 1, 0
       0, 0, 1
    T=1
    R= 1, 0, 0
       0,-1, 0
       0, 0, 1
    T=-1
    R= 0,-1, 0
       1, 0, 0
       0, 0, 1
    T=-1
    R= 0, 1, 0
      -1, 0, 0
       0, 0, 1
    T=-1
    R= 0, 1, 0
      -1, 0, 0
       0, 0,-1
    T=-1
    R= 0,-1, 0
       1, 0, 0
       0, 0,-1
symmetry operations that need to be removed= {1, 2, 5, 6, 8, 9, 12, 13}
Next we print all symmetry operations that are present for spin-up or spin-down calculation only: 

Symmetry operations left:
0 : Time=1 I
 1 0 0 0.00000000
 0 1 0 0.00000000
 0 0 1 0.00000000
1 : Time=1 R
-1 0 0 0.00000000
 0-1 0 0.00000000
 0 0 1 0.00000000
2 : Time=1 P
-1 0 0 0.00000000
 0-1 0 0.00000000
 0 0-1 0.00000000
3 : Time=1 R
 1 0 0 0.00000000
 0 1 0 0.00000000
 0 0-1 0.00000000
4 : Time=-1 R
 0 1 0 0.00000000
 1 0 0 0.00000000
 0 0-1 0.00000000
5 : Time=-1 R
 0-1 0 0.00000000
-1 0 0 0.00000000
 0 0-1 0.00000000
6 : Time=-1 R
 0-1 0 0.00000000
-1 0 0 0.00000000
 0 0 1 0.00000000
7 : Time=-1 R
 0 1 0 0.00000000
 1 0 0 0.00000000
 0 0 1 0.00000000
Hence, we keep T[1]==C2(z), T[2]==inversion=P, T[4]==C2(110), and their combinations: T[3]=C2(z)*P, T[6]=C2(1,1,0)*P, T[5]=C2(1,1,0)*C2(z), T[7]=C2(1,1,0)*C2(z)*P.
We dropped C2(x)+(1/2,1/2,1/2), C2(y)+(1/2,1/2,1/2), C2(x)*P+(1/2,1/2,1/2), C2(y)*P+(1/2,1/2,1/2), C4++(1/2,1/2,1/2), C4-(z)+(1/2,1/2,1/2), C4+(z)*P+(1/2,1/2,1/2), C4-(z)*P+(1/2,1/2,1/2), because they were transforming spin-up Ru in spin-down Ru.

Next we determine equivalency for non-magnetic atoms using shells of neighboring atoms as a test. This algorithm mirrors w2k-nn algorithm, which also looks at all neighbors to determine equivalency.
At the first iteration we have the following atoms and their neighbors: 
Going over all neighbors to determine equivalency:
....
neigbors of inequivalent atom types after iteration 1
   Ru1 ['1.941 O1 O1', '1.984 O1 O1 O1 O1', '3.106 Ru1 Ru1', '3.408 O1 O1 O1 O1', '3.536 Ru2 Ru2 Ru2 Ru2 Ru2 Ru2 Ru2 Ru2', '3.663 O1 O1 O1 O1', '4.034 O1 O1 O1 O1 O1 O1 >
   Ru2 ['1.941 O1 O1', '1.984 O1 O1 O1 O1', '3.106 Ru2 Ru2', '3.408 O1 O1 O1 O1', '3.536 Ru1 Ru1 Ru1 Ru1 Ru1 Ru1 Ru1 Ru1', '3.663 O1 O1 O1 O1', '4.034 O1 O1 O1 O1 O1 O1 >
   O1 ['1.941 Ru1', '1.984 Ru2 Ru2', '2.47 O1', '2.776 O1 O1 O1 O1 O1 O1 O1 O1', '3.106 O1 O1', '3.254 O1 O1', '3.408 Ru1 Ru1', '3.663 Ru1 Ru1', '3.882 O1', '3.969 O1 O1>
This shows that Ru1 atom has two O1 atoms at the distance of 1.941, and 4 O1 atoms at 1.984, etc. Next we recursively add more and more splitting between atoms until no more splitting is needed. At the first pass we realize that two O1 atoms can not be equivalent, because one has Ru2 at distance 1.941, and the other Ru1. 
atom[ 3] with name=O1 neigbr= ['1.941 Ru2', '1.984 Ru1 Ru1', '2.47 O1', '2.776 O1 O1 O1 O1 O1 O1 O1 O1', '3.106 O1 O1', '3.254 O1 O1', '3.408 Ru2 Ru2', '3.663 Ru2 Ru2', >
atom[ 3] with name=O1 expect= ['1.941 Ru1', '1.984 Ru2 Ru2', '2.47 O1', '2.776 O1 O1 O1 O1 O1 O1 O1 O1', '3.106 O1 O1', '3.254 O1 O1', '3.408 Ru1 Ru1', '3.663 Ru1 Ru1', >
We thus split O1 into O1 and O2. We arrive at the following splitting 
   Ru1 ['1.941 O1 O1', '1.984 O2 O2 O2 O2', '3.106 Ru1 Ru1', '3.408 O1 O1 O1 O1', '3.536 Ru2 Ru2 Ru2 Ru2 Ru2 Ru2 Ru2 Ru2', '3.663 O1 O1 O1 O1', '4.034 O2 O2 O2 O2 O2 O2 >
   Ru2 ['1.941 O2 O2', '1.984 O1 O1 O1 O1', '3.106 Ru2 Ru2', '3.408 O2 O2 O2 O2', '3.536 Ru1 Ru1 Ru1 Ru1 Ru1 Ru1 Ru1 Ru1', '3.663 O2 O2 O2 O2', '4.034 O1 O1 O1 O1 O1 O1 >
   O1 ['1.941 Ru1', '1.984 Ru2 Ru2', '2.47 O1', '2.776 O2 O2 O2 O2 O2 O2 O2 O2', '3.106 O1 O1', '3.254 O1 O1', '3.408 Ru1 Ru1', '3.663 Ru1 Ru1', '3.882 O1', '3.969 O1 O1>
   O2 ['1.941 Ru2', '1.984 Ru1 Ru1', '2.47 O2', '2.776 O1 O1 O1 O1 O1 O1 O1 O1', '3.106 O2 O2', '3.254 O2 O2', '3.408 Ru2 Ru2', '3.663 Ru2 Ru2', '3.882 O2', '3.969 O2 O2>
To determine equivalency, we measure distance between atoms, and keep three digits after the dot. i.e, 1.941 (in units of angstroms). Sometimes we need to either increase this precision or reduce it, depending on how precise are positions given in the original structure. Most of the time, the three digits work, but if there is discrepancy between these equivalent atoms, and w2k-nn routine, we need to change this number. This can be done through parameter "-p NDECIMALS", which is "NDECIMALS=3" by default.
The other parameter that could potentially need to be changed is "-R NRADIUS, --nradius=NRADIUS". By default we check neighbors up to 4.7A away from each atom. This is almost always enough to determine equivalency. But if discrepancy between w2k-nn and this algorithm occurs, one can check that this radius is sufficient. Note that in w2k we give parameter in terms of number of shells for nn.

Finally, we determine the grouping of all atoms into equivalent sets. We have: 
mgroups= [[[0], [1]], [[2, 5], [3, 4]]]
which means that Ru atoms are split into [0],[1], while oxygen atoms of the original structure file are split into O1=[2,5] group O2=[3,4].

In w2k we will list atoms consequently and O1 will appear as atoms [2,3] and O2 as [4,5]. We now reorder atoms so as they will appear in w2k structure file: 
all_sites_order= [0, 1, 2, 5, 3, 4]
Next we go over all first atoms in the w2k structure file, and check which are their neighbors. For example: 
ATOM:   1 Ru  AT   0.00000   0.00000   0.00000=  0.00000   0.00000   0.00000
nn_distance= 1.9412419687117457 Rmt[0]= 1.037157052833468
  ATOM:  5 O     AT  -1.37267  -1.37267  -0.00000= -0.30558  -0.30558   0.00000 IS AWAY      1.941242      1.941242 ANG
  ATOM:  2 O     AT   1.37267   1.37267   0.00000=  0.30558   0.30558   0.00000 IS AWAY      1.941242      1.941242 ANG
  ATOM:  3 O     AT  -0.87333   0.87333  -1.55305= -0.19442   0.19442  -0.50000 IS AWAY      1.984286      1.984286 ANG
  ATOM:  3 O     AT  -0.87333   0.87333   1.55305= -0.19442   0.19442   0.50000 IS AWAY      1.984286      1.984286 ANG
  ATOM:  4 O     AT   0.87333  -0.87333  -1.55305=  0.19442  -0.19442  -0.50000 IS AWAY      1.984286      1.984286 ANG
  ATOM:  4 O     AT   0.87333  -0.87333   1.55305=  0.19442  -0.19442   0.50000 IS AWAY      1.984286      1.984286 ANG
  ATOM:  0 Ru    AT   0.00000   0.00000  -3.10610=  0.00000   0.00000  -1.00000 IS AWAY      3.106100      3.106100 ANG
  ATOM:  0 Ru    AT   0.00000   0.00000   3.10610=  0.00000   0.00000   1.00000 IS AWAY      3.106100      3.106100 ANG
  ATOM:  5 O     AT  -1.37267   3.11933   0.00000= -0.30558   0.69442   0.00000 IS AWAY      3.407999      3.407999 ANG
  ATOM:  2 O     AT  -3.11933   1.37267  -0.00000= -0.69442   0.30558   0.00000 IS AWAY      3.407999      3.407999 ANG
  ATOM:  5 O     AT   3.11933  -1.37267   0.00000=  0.69442  -0.30558   0.00000 IS AWAY      3.407999      3.407999 ANG
  ATOM:  2 O     AT   1.37267  -3.11933  -0.00000=  0.30558  -0.69442   0.00000 IS AWAY      3.407999      3.407999 ANG
  ATOM:  1 Ru    AT  -2.24600  -2.24600  -1.55305= -0.50000  -0.50000  -0.50000 IS AWAY      3.535675      3.535675 ANG
  ATOM:  1 Ru    AT  -2.24600  -2.24600   1.55305= -0.50000  -0.50000   0.50000 IS AWAY      3.535675      3.535675 ANG
  ATOM:  1 Ru    AT  -2.24600   2.24600  -1.55305= -0.50000   0.50000  -0.50000 IS AWAY      3.535675      3.535675 ANG
  ATOM:  1 Ru    AT  -2.24600   2.24600   1.55305= -0.50000   0.50000   0.50000 IS AWAY      3.535675      3.535675 ANG
  ATOM:  1 Ru    AT   2.24600  -2.24600  -1.55305=  0.50000  -0.50000  -0.50000 IS AWAY      3.535675      3.535675 ANG
  ATOM:  1 Ru    AT   2.24600  -2.24600   1.55305=  0.50000  -0.50000   0.50000 IS AWAY      3.535675      3.535675 ANG
  ATOM:  1 Ru    AT   2.24600   2.24600  -1.55305=  0.50000   0.50000  -0.50000 IS AWAY      3.535675      3.535675 ANG
  ATOM:  1 Ru    AT   2.24600   2.24600   1.55305=  0.50000   0.50000   0.50000 IS AWAY      3.535675      3.535675 ANG
  ATOM:  5 O     AT  -1.37267  -1.37267  -3.10610= -0.30558  -0.30558  -1.00000 IS AWAY      3.662824      3.662824 ANG
  ATOM:  5 O     AT  -1.37267  -1.37267   3.10610= -0.30558  -0.30558   1.00000 IS AWAY      3.662824      3.662824 ANG
  ATOM:  2 O     AT   1.37267   1.37267  -3.10610=  0.30558   0.30558  -1.00000 IS AWAY      3.662824      3.662824 ANG
  ATOM:  2 O     AT   1.37267   1.37267   3.10610=  0.30558   0.30558   1.00000 IS AWAY      3.662824      3.662824 ANG
We list first the atom number, the symbol, the vector between the two atoms in cartesian coordinates, the vector between the two atoms in fractional coordinates, and finally the distance in angstroms.

The high-symmetry k-path proposed by pymatgen is give by 
high symmetry kpath=
\Gamma  [0.0, 0.0, 0.0]
A       [0.5, 0.5, 0.5]
M       [0.5, 0.5, 0.0]
R       [0.0, 0.5, 0.5]
X       [0.0, 0.5, 0.0]
Z       [0.0, 0.0, 0.5]
and we will produce case.klist_band with these k-points.

Next we list information about the structure we just found, as appropriate for findsym. In rare cases, in which the current algorithm could fail, one could check with findsym, the appropriate space group and new cif file. We list the information in the way that allows direct copy/paste in findsym: 
conventional unit cell (cif.w2k_coords) for finsym: https://stokes.byu.edu/iso/findsym.php:
cartesian coordinates of the basis vectors:
  4.49200   0.00000   0.00000 
 -0.00000   4.49200   0.00000 
  0.00000   0.00000   3.10610 

Number of atoms in the unit cell:  6
Type of each atom in the unit cell: 1*Ru1  1*Ru2  2*O1  2*O2 
  0.000000   0.000000   0.000000
  0.500000   0.500000   0.500000
  0.305580   0.305580   0.000000
  0.694420   0.694420   0.000000
  0.805580   0.194420   0.500000
  0.194420   0.805580   0.500000
If the bravais lattice is F, B, or C, some atoms need to be removed from w2k structure file (those that do not appear in primitive unit cell). We next remove those not in primitive cell. For RuO2 with primitive bravais lattice, nothing is removed: 
After removing atoms not in primitive cell, we have the following cif.w2k_coords list:
name=Ru1 Z=44 [0. 0. 0.]
name=Ru2 Z=44 [0.5 0.5 0.5]
name=O1 Z=8 [0.30558 0.30558 0.     ]
name=O1 Z=8 [0.69442 0.69442 0.     ]
name=O2 Z=8 [0.80558 0.19442 0.5    ]
name=O2 Z=8 [0.19442 0.80558 0.5    ]
Next we compare the choice of the unit cell between pymatgen and wien2k conventional cell (later we will also compare it to VESTA plotting program). We have 
pymatgen_conventional=
  8.48865   0.00000   0.00000  ==a1
 -0.00000   8.48865   0.00000  ==a2
  0.00000   0.00000   5.86968  ==a3
paymatgen_Unit cell volume= 422.9524415348472

primitive or simple lattice

w2k_conventional=
  8.48865   0.00000   0.00000  ==a1
  0.00000   8.48865   0.00000  ==a2
  0.00000   0.00000   5.86968  ==a3
Unit cell volume= 422.95244153484725
Ortho= True
In wien2k we also have primitive reciprocal cell, which is called BR2, and appears next: 
BR2=
  0.74019  -0.00000  -0.00000 
  0.00000   0.74019  -0.00000 
  0.00000   0.00000   1.07045 

gbas=
  0.11780  -0.00000  -0.00000 
  0.00000   0.11780  -0.00000 
  0.00000   0.00000   0.17037
gbas is BR2 divided by (2*pi) and finally, w2k primitive call is called rbas, and is inverse of gbas: 
w2k_primitive(rbas)=
  8.48865   0.00000   0.00000  ==a1
  0.00000   8.48865   0.00000  ==a2
  0.00000   0.00000   5.86968  ==a3
There is one more concept in w2k, namely, the transformation from primitive reciprocal to conventional reciprocal lattice. Namely, in primitive unit cell the momentum points of the 1BZ are simply given by k=n_1/N_1*b_1 + n_2/N_2*b_2 + n_3/N_3*b_3, where b1,b2,b3 are reciprocal vectors, and n_i goes between 0 and N_i-1. However, w2k uses (in case.klist and case.klist_band) momentum points written in conventional unit cell notation, hence these momentum points are normally transformed to conventional unit cell by k2icartes*k, and the case.klist file list k2icartes*k rather than k. The transformation is k2icartes, which is here just unity: 
k2icartes=
  1   0   0 
  0   1   0 
  0   0   1
We next print the momentum points for the special k-path both in primitive notation (used by VASP) and conventional (used by w2k) unit cell: 
Kpoints in the mesh:
\Gamma     k-PBZ=[     0,     0,     0] k-conBZ=[     0,     0,     0]
A          k-PBZ=[   0.5,   0.5,   0.5] k-conBZ=[   0.5,   0.5,   0.5]
M          k-PBZ=[   0.5,   0.5,     0] k-conBZ=[   0.5,   0.5,     0]
R          k-PBZ=[     0,   0.5,   0.5] k-conBZ=[     0,   0.5,   0.5]
X          k-PBZ=[     0,   0.5,     0] k-conBZ=[     0,   0.5,     0]
Z          k-PBZ=[     0,     0,   0.5] k-conBZ=[     0,     0,   0.5]
suggested and actual number of momentum points: 300 300 [72, 51, 63, 51, 63]
The last sentence shows that we have chosen 300 k-points, with 72 between A-M and 63 between X-Z.

Next we go one more time through all neighbors and find the best local coordinate axis for each correlated atom. The local axis is chosen by finding the polyhedra of neighbors around each atom, and for each polyhedra there exist a choice of axis such that the Green's function and hybridization has the smallest off-diagonal terms. We have to do this optimization to reduce the sign problem of Monte Carlo impurity sampling.
We first analize Ru1 at the origin: 
Analizing Ru1 at [0. 0. 0.] with N= 6
  with neigbrs:
  n[0]= [1.9412419687117457, 'O', array([-0.30558, -0.30558,  0.     ]), 0]
  n[1]= [1.941241968711747, 'O', array([0.30558, 0.30558, 0.     ]), 0]
  n[2]= [1.9842860402038462, 'O', array([-0.19442,  0.19442, -0.5    ]), 0]
  n[3]= [1.984286040203846, 'O', array([-0.19442,  0.19442,  0.5    ]), 0]
  n[4]= [1.9842860402038465, 'O', array([ 0.19442, -0.19442, -0.5    ]), 0]
  n[5]= [1.9842860402038462, 'O', array([ 0.19442, -0.19442,  0.5    ]), 0]
poly_sizes= {3, 4, 5, 6, 8, 12} group size= [2 6]
phi=
   0.0  180.0   90.0   90.0   90.0   90.0 
 180.0    0.0   90.0   90.0   90.0   90.0 
  90.0   90.0    0.0  103.0   77.0  180.0 
  90.0   90.0  103.0    0.0  180.0   77.0 
  90.0   90.0   77.0  180.0    0.0  103.0 
  90.0   90.0  180.0   77.0  103.0    0.0 
trying octahedra      : accuracy  0.055 -N= 0.012 -= 0.235
trying trigonal prism : accuracy  0.950 -N= 0.975 -= 0.000
Found the environment is octahedra  (=    0.012,=    0.235)
singular values= [1.10686883 1.         0.88025075]
# neigbors used to determine poly: (0, 6)
Rotation to input into case.indmfl by locrot=-1 : 

  0.70710678   0.70710678   0.00000000 
 -0.50000000   0.50000000  -0.70710678 
 -0.50000000   0.50000000   0.70710678 

Rotation in fractional coords : 

  0.15741469   0.15741469   0.00000000 
 -0.11130899   0.11130899  -0.22765100 
 -0.11130899   0.11130899   0.22765100 

Rotation for VESTA coords : 

  0.70710678   0.70710678   0.00000000 
 -0.50000000   0.50000000  -0.70710678 
 -0.50000000   0.50000000   0.70710678
We try polyhedra with size 3,4,5,6,8 and 12, and among them octahedra and trigonal prism are the best fit. The polyhedron with the smallest number "accuracy" wins, and here octahedra is the best match. The mismatch between the actual and expected angles is 0.235 and actual and expected distances is 0.012. Next we list the 3x3 rotation, which is used in case.indmfl and case.indmfldn file. It is rotation from the global to the local coordinate axis, written in w2k cartesian coordinates. Since the choice of cartesian coordinates depend on the choice of three axis in 3D, w2k and VESTA and pymatgen all choose different convention. To help the user picture the choice of the local axis, we print the same 3x3 rotation, but written in fractional coordinates. Here rows are e_x, e_y and e_z. Hence e_x=[0.15741469,0.15741469,0.00000000] and e_z=[-0.11130899,0.11130899,0.22765100]. These can be entered in VESTA as vectors attached to a given atom, to understand the choice of the local coordinate axis. We also give these vectors in VESTA cartesian coordinates, which one can compare with what VESTA recognizes when typing fractional coordinates.

To get proper symmetry in altermagnets, it is essential to choose local axis on the opposite atoms (the one with opposite spin) using the symmetry operation that flips the spin. As discussed above, we have 8 possibilities which all flip the spins and all are accompanied by translation for (1/2,1/2,1/2), i.e., C2(x), C2(y), C2(x)*P, C2(y)*P, C4+(z), C4-(z), C4+(z)*P, C4-(z)*P. We are going to try successive transformation and use them to transform axis. Here C2(x) can be used, and is being used 
We are trying to use transformed local axis of Ru1 for atom Ru2
positions of neigbors around Ru1 which we are checking:
    [ -0.305580, -0.305580,  0.000000]
    [  0.305580,  0.305580,  0.000000]
    [ -0.194420,  0.194420, -0.500000]
    [ -0.194420,  0.194420,  0.500000]
    [  0.194420, -0.194420, -0.500000]
    [  0.194420, -0.194420,  0.500000]
using rotation:
    [ 1, 0, 0]
    [ 0,-1, 0]
    [ 0, 0,-1]
transformed positions of neigbors around Ru2 which we are checking:
    [ -0.305580, -0.305580,  0.000000]
    [  0.305580,  0.305580,  0.000000]
    [  0.194420, -0.194420, -0.500000]
    [ -0.194420,  0.194420, -0.500000]
    [  0.194420, -0.194420,  0.500000]
    [ -0.194420,  0.194420,  0.500000]
atom[0] -> atom[0] with accuracy= 5.551115123125783e-17
atom[1] -> atom[1] with accuracy= 5.551115123125783e-17
atom[4] -> atom[2] with accuracy= 5.551115123125783e-17
atom[2] -> atom[3] with accuracy= 5.551115123125783e-17
atom[5] -> atom[4] with accuracy= 5.551115123125783e-17
atom[3] -> atom[5] with accuracy= 5.551115123125783e-17
Works= True
Accepting above transformation to transform local axis of Ru1 to axis of Ru2 at  [0.5 0.5 0.5]
Using transformation:
    [  1.000000,  0.000000,  0.000000]
    [  0.000000, -1.000000,  0.000000]
    [  0.000000,  0.000000, -1.000000]
# neigbors used to determine poly: (0, 6)
Rotation to input into case.indmfl by locrot=-1 : 

  0.70710678  -0.70710678  -0.00000000 
 -0.50000000  -0.50000000   0.70710678 
 -0.50000000  -0.50000000  -0.70710678 

Rotation in fractional coords : 

  0.15741469  -0.15741469  -0.00000000 
 -0.11130899  -0.11130899   0.22765100 
 -0.11130899  -0.11130899  -0.22765100 

Rotation for VESTA coords : 

  0.70710678  -0.70710678  -0.00000000 
 -0.50000000  -0.50000000   0.70710678 
 -0.50000000  -0.50000000  -0.70710678
As can be verified, our e_x, e_y and e_z all have their y and z components with opposite sign, while the x component keeps its sign, because we use C2(x).

Finally, we try to find how many impurity problems are necessary to simulate this material. 
cix2atom= {1: 1, 2: 2}
remain= [0, 1]
flipping[atom=2,icix=2]=atom=1,icix=1
remain at the end= []
nf0[Ru]= 7  atomic configuration= 7  oxidation= 0
We see that atom=1 and atoms=2 will have icix=1 and icix=2 in case.indmfl file. We have [0,1] as correlated atoms. But we then realize that atom=2,icix=2 can be spin-flipped to obtain atom=1,icix=1, hence we actually need to simulate only one impurity. When all impurities can be grouped by flipping, we write "remain at the end=[]".
Finally, we also list what is default number of electrons expected on this atom (ignoring oxidation state). We will later take occupancy from DFT, and this number will be hence overwritten anyway.

Next we check the content of eDMFT input files. We start with 0_607_RuO2.indmfi: 
1   # number of sigind blocks
10   # dimension of this sigind block
 1  0  0  0  0  0  0  0  0  0 
 0  2  0  0  0  0  0  0  0  0 
 0  0  3  0  0  0  0  0  0  0 
 0  0  0  4  0  0  0  0  0  0 
 0  0  0  0  5  0  0  0  0  0 
 0  0  0  0  0  6  0  0  0  0 
 0  0  0  0  0  0  7  0  0  0 
 0  0  0  0  0  0  0  8  0  0 
 0  0  0  0  0  0  0  0  9  0 
 0  0  0  0  0  0  0  0  0 10
It means we have one impurity problem with diagonal hybridizations enumerated from 1-10, hence we do not have spin-up down symmetry.

Next we check 0_607_RuO2.indmfl, which contains: 
0 0 1 5                               # hybridization band index nemin and nemax, renormalize for interstitials, projection type
1 0.025 0.025 200 -3.000000 1.000000  # matsubara, broadening-corr, broadening-noncorr, nomega, omega_min, omega_max (in eV)
2                                     # number of correlated atoms
1     1  -1                           # iatom, nL, locrot
  2   2   1                           # L, qsplit, cix
 0.70710678  0.70710678  0.00000000   # new x-axis
-0.50000000  0.50000000 -0.70710678   # new y-axis
-0.50000000  0.50000000  0.70710678   # new z-axis
2     1  -1                           # iatom, nL, locrot
  2   2   2                           # L, qsplit, cix
 0.70710678 -0.70710678 -0.00000000   # new x-axis
-0.50000000 -0.50000000  0.70710678   # new y-axis
-0.50000000 -0.50000000 -0.70710678   # new z-axis
#================ # Siginds and crystal-field transformations for correlated orbitals ================
2     5   5       # Number of independent kcix blocks, max dimension, max num-independent-components
1     5   5       # cix-num, dimension, num-independent-components
#---------------- # Independent components are --------------
'z^2' 'x^2-y^2' 'xz' 'yz' 'xy' 
#---------------- # Sigind follows --------------------------
1 0 0 0 0
0 2 0 0 0
0 0 3 0 0
0 0 0 4 0
0 0 0 0 5
#---------------- # Transformation matrix follows -----------
 0.00000000  0.00000000    0.00000000  0.00000000    1.00000000  0.00000000    0.00000000  0.00000000    0.00000000  0.00000000  
 0.70710678  0.00000000    0.00000000  0.00000000    0.00000000  0.00000000    0.00000000  0.00000000    0.70710678  0.00000000  
 0.00000000  0.00000000    0.70710678  0.00000000    0.00000000  0.00000000   -0.70710678  0.00000000    0.00000000  0.00000000  
 0.00000000  0.00000000    0.00000000  0.70710678    0.00000000  0.00000000    0.00000000  0.70710678    0.00000000  0.00000000  
 0.00000000  0.70710678    0.00000000  0.00000000    0.00000000  0.00000000    0.00000000  0.00000000   -0.00000000 -0.70710678  
2     5   5       # cix-num, dimension, num-independent-components
#---------------- # Independent components are --------------
'z^2' 'x^2-y^2' 'xz' 'yz' 'xy' 
#---------------- # Sigind follows --------------------------
 6  0  0  0  0
 0  7  0  0  0
 0  0  8  0  0
 0  0  0  9  0
 0  0  0  0 10
#---------------- # Transformation matrix follows -----------
 0.00000000  0.00000000    0.00000000  0.00000000    1.00000000  0.00000000    0.00000000  0.00000000    0.00000000  0.00000000  
 0.70710678  0.00000000    0.00000000  0.00000000    0.00000000  0.00000000    0.00000000  0.00000000    0.70710678  0.00000000  
 0.00000000  0.00000000    0.70710678  0.00000000    0.00000000  0.00000000   -0.70710678  0.00000000    0.00000000  0.00000000  
 0.00000000  0.00000000    0.00000000  0.70710678    0.00000000  0.00000000    0.00000000  0.70710678    0.00000000  0.00000000  
 0.00000000  0.70710678    0.00000000  0.00000000    0.00000000  0.00000000    0.00000000  0.00000000   -0.00000000 -0.70710678
We notice that local rotations are already properly set. The first atom has hybridization components 1-5, and the second 6-10. We encourage the user to now check 0_607_RuO2.indmfldn file, which exchanges hybridization components, so that the first atom contains indices 6-10 and the second 1-5. Using this symmetry, we manage to descrive the two site problem with solving a single impurity problem.

A careful reader will see that the first line of indmfl file should list the index of the bands which are augmented with eDMFT. Currently these indices are set to "0 0". The reason for this is that we did not yet perform DFT calculation to know the energy of bands, hence we can finish this initialization only once the DFT program has finished successfully.

Finally, the "params.dat" file is: 
solver              ='CTQMC'         # impurity solver
DCs                 ='exacty'        # double counting scheme
max_dmft_iterations =1               # number of iteration of the dmft-loop only
max_lda_iterations  =100             # number of iteration of the LDA-loop only
finish              =50              # number of iterations of full charge loop (1 = no charge self-consistency
ntail               =300             # on imaginary axis, number of points in the tail of the logarithmic mesh
cc                  =1e-05           # the charge density precision to stop the LDA+DMFT run
ec                  =1e-05           # the energy precision to stop the LDA+DMFT run
recomputeEF         =1               # Recompute EF in dmft2 step. If recomputeEF = 2, it tries to find an insulating gap.

# Impurity problem number 0
iparams0={
     "exe"               : ["ctqmc"        , "# Name of the executable"],
     "U"                 : [6.0            , "# Coulomb repulsion (F0) for Ru"],
     "J"                 : [0.8            , "# Hunds coupling  (J) for Ru"],
     "CoulombF"          : ["'Ising'"      , "# Can be set to Full"],
     "beta"              : [50             , "# Inverse temperature"],
     "svd_lmax"          : [30             , "# We will use SVD basis to expand G, with this cutoff"],
     "M"                 : [5000000        , "# Total number of Monte Carlo steps"],
     "mode"              : ["SH"           , "# We will use self-energy sampling, and Hubbard I tail"],
     "nom"               : [250            , "# Number of Matsubara frequency points sampled"],
     "tsample"           : [400            , "# How often to record measurements"],
     "GlobalFlip"        : [1000000        , "# How often to try a global flip"],
     "warmup"            : [300000         , "# Warmup number of QMC steps"],
     "nf0"               : [7              , "# Nominal occupancy nd for double-counting"],
}
Here we choose "exacty"-double-counting, and U=6, J=0.8, and Ising form of the Coulomb repulsion.

We next proceed to DFT calculation. Wien2k non-magnetic calculation should be performed next. We will choose GGA functional (#13). During initialization wien2k might complain that space group is not compatible with bravais lattice: 
Number and name of space group: 65 (C m m m)
warning: !!! Bravais lattice has changed.
because we used non-magnetic space group from mcif file, while w2k wants to use another space group. But we should not accept w2k suggestion here. If we accept w2k structure, we would need to change case.indmfl file and case.indmfldn file, because the local axis choice will no longer be appropriate. We therefore want to avoid any transformation of the structure file by wien2k. We can run initialization in batch mode, i.e., 
init_lapw -b -red 0 -vxc 13 -ecut -7.0  -numk 80
followed by 
run_lapw
Now that we have DFT band-structure (the band energies for hybridization window) and occupancy (for default nf0 in double-counting) we finish eDMFT initialization. We execute 
init_proj.py  -a
which gives the following information 
INFO: case.indmfldn present => magnetic calculation with two dmft2 steps
Computing DMFT real space projector, which is written in projectorw.dat
atm_l_case= {0: ([2], 0), 1: ([2], 0)}
opening 0_607_RuO2.scf2
EF= 8.27056097924597 eV =  0.6078750733 Ry
dx= 0.015622910177195711
Rx[:]= 1e-05 1.9600000000000009 1.9600000000000009
using E= 0.6078750733
dx= 0.015622910177195711
Rx[:]= 1e-05 1.9600000000000009 1.9600000000000009
using E= 0.6078750733
Going over all case.energy files to find which bands are used to construct DMFT projector
Number of all atoms found in struct file 4
file: 0_607_RuO2.energy nemin= 13 nemax= 36
Finally set nemin= 13 nemax= 36
Found dft-occupancy[icix=1]= 4.5369
Found dft-occupancy[icix=2]= 4.5347
Impurity-lattice connection: imp2latt= {0: [1, 2]}
Finally nf0= {0: 5}
orig=      "nf0"               : [7              , "# Nominal occupancy nd for double-counting"],
repl=      "nf0"               : [5              , "# Nominal occupancy nd for double-counting"],
This output says that eDMFT will augment bands 13-36, hence this will become first line in case.indmfl and case.indmfldn file. The DFT occupancy is way smaller than atomic value 7, hence nf0 will be set to the closest integer, which is here 5.

Finally we also initialize self-energy with finite spin splitting. To do that, we use option "-m". 
~/dbin/szero.py -m
This option works for very simple cases like RuO2, however, it does not always work, and one should carefully consider what is the best choice of starting self-energy splitting. In this particular case we choose self-energy at infinity (s_oo) to be 1eV lower for first five orbitals, and 1eV higher for the second five orbitals, i.e., 
# s_oo= [24.4, 24.4, 24.4, 24.4, 24.4, 26.4, 26.4, 26.4, 26.4, 26.4]
#  Edc= [25.4, 25.4, 25.4, 25.4, 25.4, 25.4, 25.4, 25.4, 25.4, 25.4]
The precise splitting is not important, and it will be adjusted during self-consistent iteration. However, a bad choice for the splitting will require many more iterations to achieve convergence. This is especially important when we have many correlated atoms and many different spin orientations. User should carefully consider which columns correspond to which atom, and than shift s_oo or different atoms according to their expected magnetic moments.

Before submitting this eDMFT run, we need to substantially increase the number of momentum points. For example, 1000 momentum points is reasonable. We do this by running: 
x kgen
  1000
We next submit the job to the supercomputer and use commensurate number of cores to the number of momentum points in case.klist file (120 in this case). Once the calculation is finished, we examine n_imp and n_latt in info.iterate, i.e., column 9 and 10. If the two values are sufficiently close, we can be confident in our choice of the orbitals.
For the RuO2 the current choice of local orbitals is ok, and here is how it should look like:
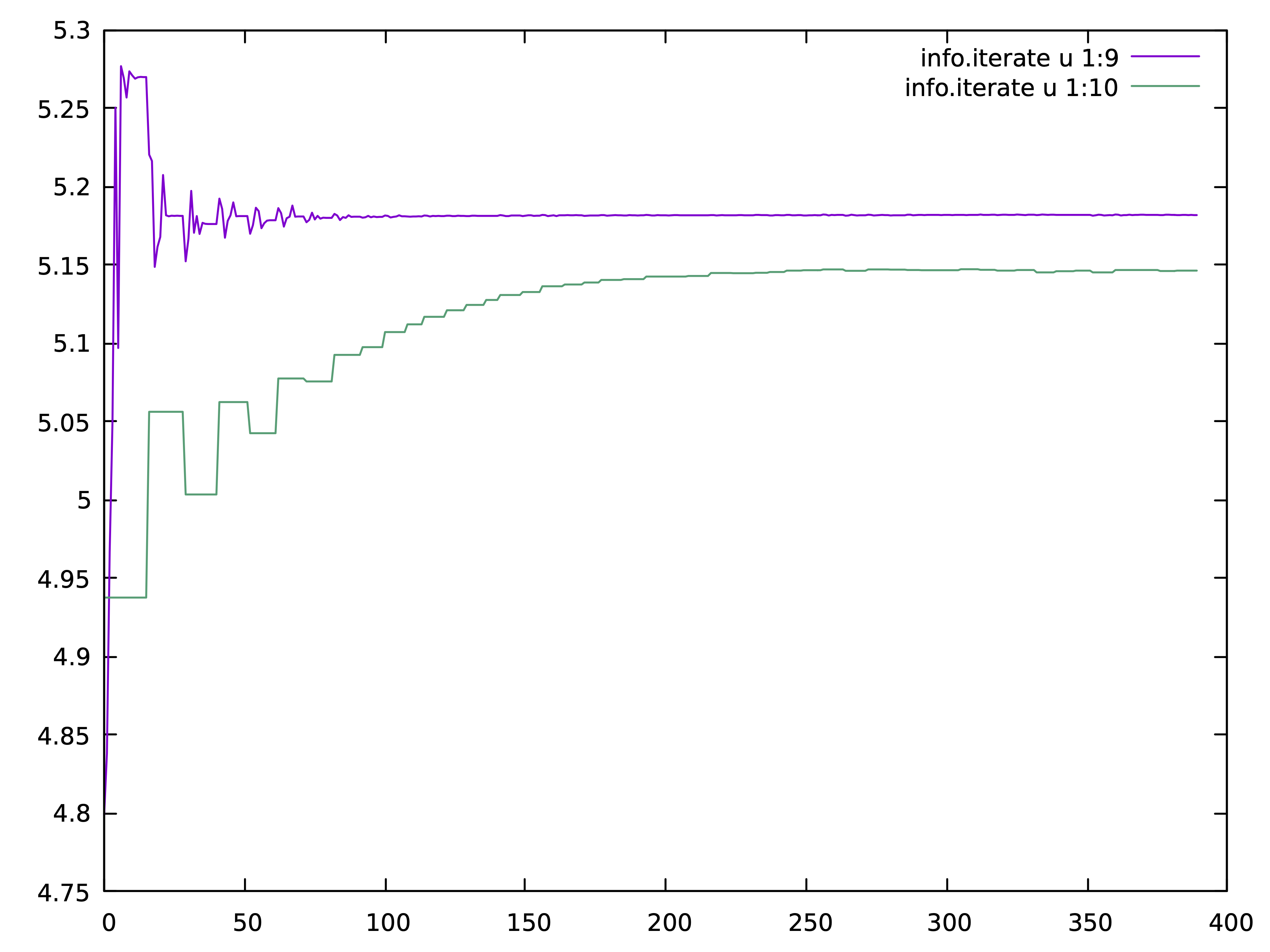The lattice density is around 5.181 and the impurity density around 5.146, which is acceptable, but later we will improve that with findRot.py script.
If the values are far off, there is either a bug, or, bad choice of local orbitals. Currently we use cubic harmonics, but we can execute "findRot.py" script on resulting calculation if the mismatch between n_imp and n_latt is too large.
Even better is to compare case.gc[1-2] and imp.0/Gf.out.50.1. This checks if the local green's function is the same as the impurity green's function. If green's function is diagonal, our choice of diagonal hybridization should make these two Green's function equal. But if hybridization is chosen to be diagonal, while the Green's function is not, we will have mismatch between the two quantities. Here is how they look like in this run for up and down spins:
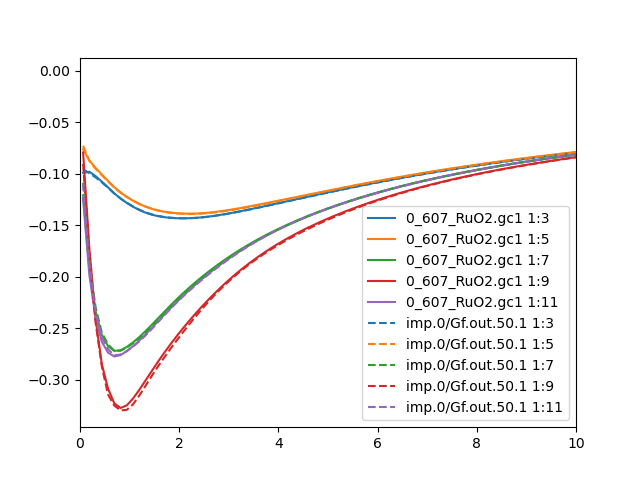
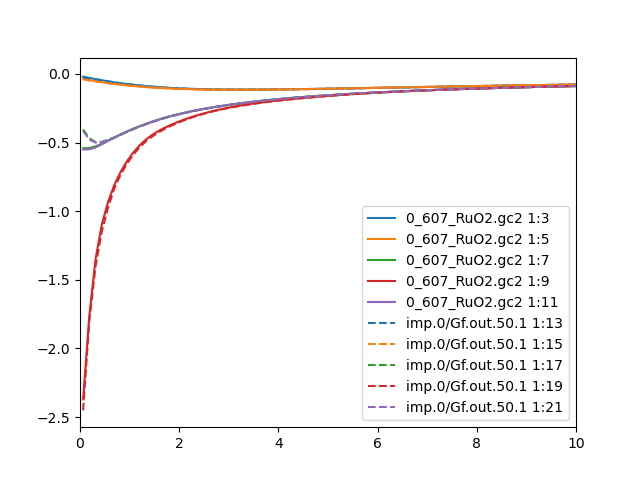Similar conclusion can be drawn from the Green's function comparison than the impurity/lattice density: the agreement is not perfect, but it is acceptable. Hence we will proceed to the analytic continuation.

We check a few last eDMFT self-energies (sig.inp.4[5-9].1 sig.inp.50.1) and we confirm that they differ only due to Monte Carlo noise. We can hence average over the last few iterations. For example: 
saverage.py sig.inp.4[5-9] sig.inp.50
to obtain "sig.inpx" averaged self-energy. Next we proceed to the maximum-entropy method that produces self-energy on the real axis.
For this example we will increase the real axis mesh to 30eV, because it turns out that in some cases 20eV default is somewhat too small window on the real axis. We also need to somewhat increase the number of points on the real axis, since the range has increase (Nw=450). The rest of the parameters are default, which we used before. The content of "maxent_params.dat" file should be set to: 
params={'statistics': 'fermi', # fermi/bose
        'Ntau'      : 400,     # Number of time points
        'L'         : 30.0,    # cutoff frequency on real axis
        'x0'        : 0.01,    # low energy cut-off
        'bwdth'     : 0.004,   # smoothing width
        'Nw'        : 450,     # number of frequency points on real axis
        'gwidth'    : 2*15.0,  # width of gaussian
        'idg'       : 1,       # error scheme: idg=1 -> sigma=deltag ; idg=0 -> sigma=deltag*G(tau)
        'deltag'    : 0.005,   # error
        'Asteps'    : 4000,    # anealing steps
        'alpha0'    : 1000,    # starting alpha
        'min_ratio' : 0.001,   # condition to finish, what should be the ratio
        'iflat'     : 1,       # iflat=0 : constant model, iflat=1 : gaussian of width gwidth, iflat=2 : input using file model.dat
        'Nitt'      : 1000,    # maximum number of outside iterations
        'Nr'        : 0,       # number of smoothing runs
        'Nf'        : 40,      # to perform inverse Fourier, high frequency limit is computed from the last Nf points
        }
We next execute 
maxent_run.py sig.inpx
and we should obtain the self-energy on the real axis "Sig.out", which should look like this:


Next we create a directory for the real axis spectra and density of states. Let's call it "onreal". We enter that subdirectory and copy all necessary files from the self-consistent run by the script 
dmft_copy.py ../
Here the argument is the name of the directory with the self-consistent run. We will compute the band structure on the real axis now. But before we run eDMFT on k-path in first BZ, we might need to fine tune the path. The default path is [\Gamma,A,M,R,X,Z] (see "cif2struct.log" or look into "0_607_RuO2.klist_band"). It turns out that this high symmetry path does not reveal the nature of altermagnetic band splitting. The splitting is largest between Gamma-M, hence we will modify the k-path to [M,\Gamma,M,A,R,X,Z]. To do that, we will execute "klist_gen.py". This script can be run interactively, or in batch mode. We will use the batch mode here: 
klist_gen.py -n 500 -p "[[0.5,0.5,0],[0,0,0],[0.5,0.5,0],[0.5,0.5,0.5],[0.,0.5,0.5],[0,0.5,0],[0,0,0.5]]" -m "['M','\Gamma','M','A','R','X','Z']"
which produces "case.klist_band", and we rename it to "0_607_RuO2.klist_band".
Now we proceed to calculation of the densities of states and bands. We execute the following set of commands in the directory "onreal": 
$WIENROOT/x_lapw lapw0 -f 0_607_RuO2 >& nohup.dat 
$WIEN_DMFT_ROOT/x_dmft.py lapw1        >& nohup.dat
$WIEN_DMFT_ROOT/x_dmft.py dmft1        >& nohup.dat
$WIEN_DMFT_ROOT/x_dmft.py lapw1 --band >& nohup.dat
$WIEN_DMFT_ROOT/x_dmft.py dmftp        >& nohup.dat
$WIEN_DMFT_ROOT/x_dmft.py dmftp -l dn  >& nohup.dat
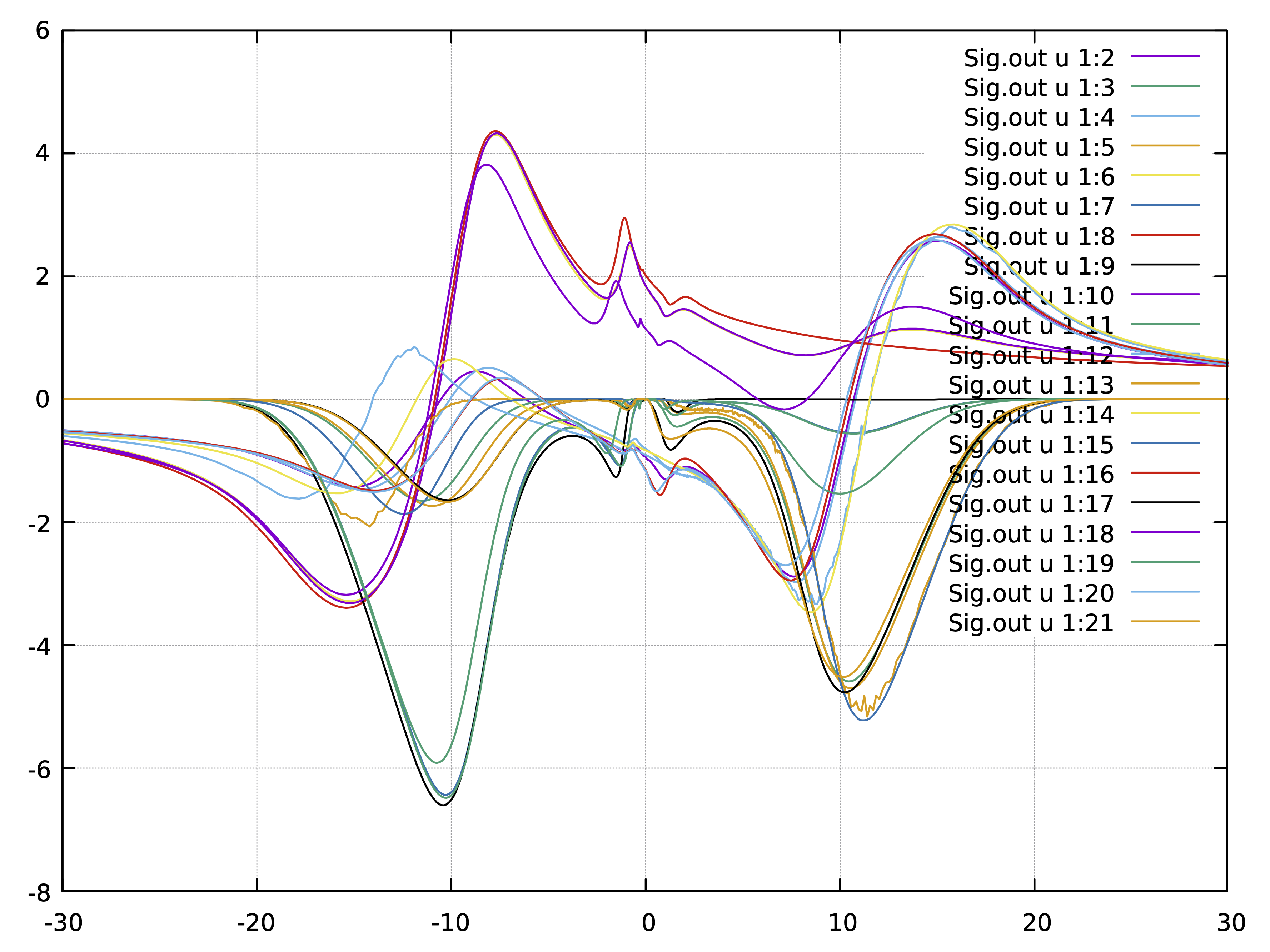
This first two produce DFT potential and DFT bands (vector file). Then dmft1 produces local density of states and green's function on the real axis. We could omit the two steps (lapw1 and dmft1) if DOS is not needed. Or, we could add another dmft1 step with "-l dn" option. The latter would produce DOS for down spins. For altermagnet the down-spins have identical DOS as the up-spins. But in ferrimagnetic or ferromagnetic materials the density of states for up and down are different, and we need additional dmft1 step. Finally, dmftp step here produces dmft eigenvalues (dmft bands) and is execute for both the up and the down spins, because the two are expected to be different in altermagnets.

Finally, we want to plot the spectral function of both the up and down spins simultaneously. We have a dedicated python script for that: 
makplot.py
which reads both "eigvals.dat" and "eigvalsdn.dat", and displays them in red-blue color, respectively. Here is how it looks like for this run:

The argument for intensity can be given to makplot.py, however, its value should be between 0-1, and a number very close to 1 is desired. Default is 0.97. Namely, in the old version of "wakplot.py" routine we would specify intensity (the argument) as the ratio between maximum value of Akw considered when plotting (the cutoff for plotting) and the maximum value found in the 2D plot. The problem with this algorithm is that sometimes intensity needs to be reduced to a very small number. Namely, it sometimes happens that a very few points (sometimes a single point) in the 2D plot are extremely singular, while majority of the relevant points have modest values distributed between [0,v_max]. But v_max in this case is much smaller than the maximum value we find in 2D plot, hence the ratio (given as input parameter) must be very small to have a reasonable plot.

In the new version of the plotting program, we obtain the histogram of values in the 2D plot, and we keep 97\% of the values in the plot, i.e., 3\% are cut-off for the purpose of the plot. If the shapes appear too broad and intense, we would increase this number closer to unity. If the quasiparticle bands appear very faint, we would decrease this value towards 0.5. But a small value for intensity in this algorithm does not make much sense. For this run, the value of 
makplot.py 0.99
sharpens up the spectra, and produces


Finally, we noticed above that lattice density and impurity density do not match perfectly at the converged solution, because the impurity problem is not completely diagonal in our chosen real harmonics basis. But we have freedom to choose any orbital basis we want, and a better basis can be often chosen by diagonalizing the hybridization function at low frequency.
The script "findRot.py" does that. It can diagonalize hybridization either at low energy, or at infinite frequency, and should substantially reduce this mismatch.
We will slightly edit the self-energy file and we will add frequency omega=0 on imaginary axis. This is not essential, but it is a good idea to diagonalize hybridization at exactly zero frequency, which is of course equal on real and imaginary axis. We will take the real part of the self-energy for each orbital from the lowest matsubara point, while we will zero out imaginary parts (because they should vanish at zero frequency in a metal). The first two lines of the data in the "sig.inp" file look like that 
0.0                      -9.299057493961586651e-01  0.0                      -7.980767955268603941e-01   0.0                     1.856077099430119670e+00 0 ....
6.283185307179600665e-02 -9.299057493961586651e-01 -2.480501738282099924e-02 -7.980767955268603941e-01 -1.601768961148599887e-02 1.856077099430119670e+00 -3.745090133373799729e-02 ...
We than execute lapw1 and dmft1 on this self-energy 
x_dmft.py  lapw1
x_dmft.py  dmft1
which will compute the density matrix and the hybridization at zero frequency and at infinite frequency. We look into "0_607_RuO2.outputdmf1" and see 
 omega~0 is  0.000000000000000E+000 at i=           1
 Full matrix of impurity levels follows
 icix=           1
   -2.19442993    -0.00000000       0.02491185    -0.00000000       0.00001048    -0.00000000      -0.10556106     0.00000000      -0.00000777     0.00000000   
    0.02491185     0.00000000      -2.22316952    -0.00000000      -0.00001503     0.00000000       0.18283159    -0.00000000       0.00001659    -0.00000000   
    0.00001048     0.00000000      -0.00001503    -0.00000000      -4.07898996    -0.00000000       0.00000261     0.00000000       0.03014284    -0.00000000   
   -0.10556106    -0.00000000       0.18283159     0.00000000       0.00000261    -0.00000000      -3.83831649     0.00000000      -0.00000261    -0.00000000   
   -0.00000777    -0.00000000       0.00001659     0.00000000       0.03014284     0.00000000      -0.00000261     0.00000000      -4.07898793     0.00000000   
 
 icix=           1 at omega=0
    2.30955442    -0.00000000      -1.99477879     0.00000000      -0.00013691     0.00000000      -0.42448657     0.00000000       0.00015658     0.00000000   
   -1.99477879    -0.00000000       4.60893257    -0.00000000       0.00030171     0.00000000       0.73482339     0.00000000      -0.00020871    -0.00000000   
   -0.00013691    -0.00000000       0.00030171    -0.00000000      -3.46926140    -0.00000000      -0.00029553     0.00000000       0.24824833    -0.00000000   
   -0.42448657    -0.00000000       0.73482339    -0.00000000      -0.00029553    -0.00000000      -3.50311324     0.00000000       0.00029820    -0.00000000   
    0.00015658    -0.00000000      -0.00020871     0.00000000       0.24824833     0.00000000       0.00029820     0.00000000      -3.46903791     0.00000000   
 
 icix=           2
   -2.19530225    -0.00000000       0.02477157    -0.00000000       0.00000775    -0.00000000      -0.10494473    -0.00000000      -0.00000479     0.00000000   
    0.02477157     0.00000000      -2.22386664     0.00000000      -0.00001001     0.00000000       0.18176118     0.00000000       0.00001172     0.00000000   
    0.00000775     0.00000000      -0.00001001    -0.00000000      -4.07979893     0.00000000       0.00000060     0.00000000       0.03043344     0.00000000   
   -0.10494473     0.00000000       0.18176118    -0.00000000       0.00000060    -0.00000000      -3.83803086    -0.00000000      -0.00000060     0.00000000   
   -0.00000479    -0.00000000       0.00001172    -0.00000000       0.03043344     0.00000000      -0.00000060    -0.00000000      -4.07979861     0.00000000   
 
 icix=           2 at omega=0
    3.09647612    -0.00000000      -1.48434905     0.00000000       0.00087385    -0.00000000      -0.00526244    -0.00000000      -0.00005241     0.00000000   
   -1.48434905    -0.00000000       4.82431354     0.00000000      -0.00055118     0.00000000       0.01001850    -0.00000000       0.00100097    -0.00000000   
    0.00087385     0.00000000      -0.00055118    -0.00000000      -2.91196068     0.00000000       0.00005605     0.00000000       0.49142684    -0.00000000   
   -0.00526244     0.00000000       0.01001850     0.00000000       0.00005605    -0.00000000      -3.44759215    -0.00000000      -0.00004601    -0.00000000   
   -0.00005241    -0.00000000       0.00100097     0.00000000       0.49142684     0.00000000      -0.00004601     0.00000000      -2.91328536     0.00000000
First line shows that the code found the zero frequency in the first line of self-energy, and it will compute the hybridization at that frequency. The first and the third matrix correspond to the impurity levels on Ru[0] and Ru[1] atom for up spins. They do not depend on the self-energy. While there is some mixing between orbitals, its mixing at infinite frequency is weak. But at zero frequency this is not the case. If we look at the matrix two and four we see large mixing between z^2 and x^2-y^2 orbital (the first two orbitals) and x^2-y^2 with yz orbital. To diagonalize this hybridization, we execute 
findRot.py
This diagonalization mostly mixes z^2 with x^2-y^2 orbital and xz with xy orbital, such that the new choice of the orbitals on the first Ru is Y_{z^2}*0.86583974+Y_{x^2-y^2}*0.49827165, and Y_{z^2}*0.50032144-0.86228814*Y_{x^2-y^2}, as well as (Y_{xz}+Y_{xy})/sqrt(2), (Y_{xz}-Y_{xy})/sqrt(2).
The script also corrected "0_607_RuO2.indmfl" file, which now has the following local orbitals on Ru[0] 
 0.35378068  0.00000504    0.00000522  0.00001678    0.86583974  0.00000000   -0.00000522  0.00001678    0.35378068 -0.00000504  
-0.60972979  0.00001695   -0.00002246 -0.06397079    0.49827165  0.00000000    0.00002246 -0.06397079   -0.60972979 -0.00001695  
 0.00020813  0.49988468   -0.50010977 -0.00233687   -0.00016978  0.00000000    0.50010977 -0.00233687    0.00020813 -0.49988468  
 0.05539642 -0.00166417    0.00165785 -0.70420329   -0.04524249  0.00000000   -0.00165785 -0.70420329    0.05539642  0.00166417  
 0.00000660 -0.50011252   -0.49988745  0.00000533    0.00000647  0.00000000    0.49988745  0.00000533    0.00000660  0.50011252
and the following on Ru[1] 
 0.35248283  0.00006914    0.00007282  0.00005369    0.86689773  0.00000000   -0.00007282  0.00005369    0.35248283 -0.00006914  
-0.61298876 -0.00006949    0.00007121 -0.00087625    0.49848571  0.00000000   -0.00007121 -0.00087625   -0.61298876  0.00006949  
 0.00004893 -0.49966294   -0.50033683 -0.00000490    0.00012396  0.00000000    0.50033683 -0.00000490    0.00004893  0.49966294  
-0.00078652  0.00084366   -0.00084945  0.70710522    0.00055202 -0.00000000    0.00084945  0.70710522   -0.00078652 -0.00084366  
 0.00008365 -0.50033611    0.49966221  0.00119733   -0.00007231 -0.00000000   -0.49966221  0.00119733    0.00008365  0.50033611
Note that each row correspond to one local orbital, but written in spherical harmonics, starting with m=-2,-1,...2.

Next we want to rerun dmft1 step, and check how diagonal are impurity levels now: 
x_dmft.py dmft1
The output in "0_607_RuO2.outputdmf1" is 
 omega~0 is  0.000000000000000E+000 at i=           1
 Full matrix of impurity levels follows
 icix=           1
   -2.18004748     0.00000000       0.00001289     0.00000000       0.00000022    -0.00000000      -0.00004107     0.00000000       0.00001917    -0.00000000   
    0.00001289    -0.00000000      -2.21263596    -0.00000000       0.00013626    -0.00000000       0.06353508    -0.00000000      -0.00001056     0.00000000   
    0.00000022     0.00000000       0.00013626     0.00000000      -4.10911936     0.00000000       0.00081448     0.00000000       0.00001455     0.00000000   
   -0.00004107    -0.00000000       0.06353508     0.00000000       0.00081448    -0.00000000      -3.86331357     0.00000000      -0.00000171     0.00000000   
    0.00001917     0.00000000      -0.00001056    -0.00000000       0.00001455    -0.00000000      -0.00000171    -0.00000000      -4.04884784     0.00000000   
 
 icix=           1 at omega=0
    1.06866021     0.00000000      -0.00490263    -0.00000000       0.00000106    -0.00000000      -0.00014357    -0.00000000       0.00004811     0.00000000   
   -0.00490263     0.00000000       5.82362525    -0.00000000      -0.00039349     0.00000000      -0.00137855     0.00000000      -0.00004948     0.00000000   
    0.00000106     0.00000000      -0.00039349    -0.00000000      -3.71341613     0.00000000       0.00045141     0.00000000       0.00015137    -0.00000000   
   -0.00014357     0.00000000      -0.00137855    -0.00000000       0.00045141    -0.00000000      -3.58091974     0.00000000       0.00000151     0.00000000   
    0.00004811    -0.00000000      -0.00004948    -0.00000000       0.00015137     0.00000000       0.00000151    -0.00000000      -3.21766437     0.00000000   
 
 icix=           2
   -2.18104942    -0.00000000      -0.00011523     0.00000000       0.00026524    -0.00000000      -0.00049293    -0.00000000      -0.00000774     0.00000000   
   -0.00011523    -0.00000000      -2.23759918     0.00000000       0.00000472     0.00000000      -0.20796699     0.00000000      -0.00061574     0.00000000   
    0.00026524     0.00000000       0.00000472    -0.00000000      -4.04936646    -0.00000000      -0.00000197    -0.00000000       0.00004117     0.00000000   
   -0.00049293    -0.00000000      -0.20796699     0.00000000      -0.00000197     0.00000000      -3.83847698    -0.00000000       0.00048766    -0.00000000   
   -0.00000774    -0.00000000      -0.00061574    -0.00000000       0.00004117    -0.00000000       0.00048766     0.00000000      -4.11017740     0.00000000   
 
 icix=           2 at omega=0
    2.24446045    -0.00000000       0.00586448     0.00000000       0.00084256    -0.00000000      -0.00046833    -0.00000000      -0.00002755     0.00000000   
    0.00586448    -0.00000000       5.62743693     0.00000000       0.00001635     0.00000000      -0.00372699    -0.00000000      -0.00449864     0.00000000   
    0.00084256     0.00000000       0.00001635    -0.00000000      -2.41907272    -0.00000000       0.00000532    -0.00000000       0.00062370    -0.00000000   
   -0.00046833     0.00000000      -0.00372699     0.00000000       0.00000532     0.00000000      -3.44784432    -0.00000000      -0.00055677    -0.00000000   
   -0.00002755    -0.00000000      -0.00449864    -0.00000000       0.00062370     0.00000000      -0.00055677     0.00000000      -3.39060635     0.00000000
which shows that both at zero and infinite frequency the hybridization is now pretty diagonal. But the hybridization is not exactly diagonal and sometimes turns out to be quite off-diagonal after using this script. This looks counterintuitive at first, as we diagonalized the matrix, and hence expect exactly diagonal result. If we use the "findRot.py" script on the DFT run, or constant self-energy, it will exactly diagonalize the hybridization. However, when using the same script on finite self-energy (or not constant self-energy), diagonalization becomes non-linear problem, because the hybridization does not only depend on the choice of the orbital, but also non-linearly on the self-energy embedded into the system. Namely, the hybridization depends non-linearly on the embedded self-energy, which is also changed by changing the local orbital basis. Therefore this diagonalization will not always work at the first step. If the resulting hybridization is still very off-diagonal, we might want to repeat the procedure. Namely call the script finRot.py again and recompute the hybridization with dmft1 step. We could repeat this for several iterations, and see if this produces more diagonal hybridization than the first step.

One more word of caution is in order. The current script "findRot.py" currently changes only case.indmfl but not case.indmfldn. Once we are happy with the choice of the orbitals in case.indmfl, we should also change orbitals in case.indmfldn accordingly. For example, orbitals 1-5 in case.indmfl should be copied to 6-10 in case.indmfldn, and viceversa.
Once we updated "0_607_RuO2.indmfl" and "0_607_RuO2.indmfldn", we copy them to the converged run, and resubmit the job, to converge it again with this superior choice of orbitals. The difference between the impurity and lattice density disappears, and info.iterate (column 9 and 10) show the following:
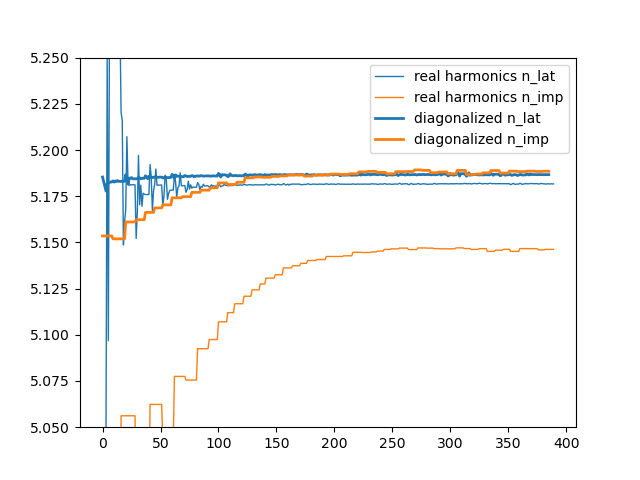We included for reference the original run with real harmonics, which is compared with this run using diagonalized local orbitals.
The Green's function mismatch is also eliminated. We plot the comparison between the impurity and lattice Green's function for both Ru sites:

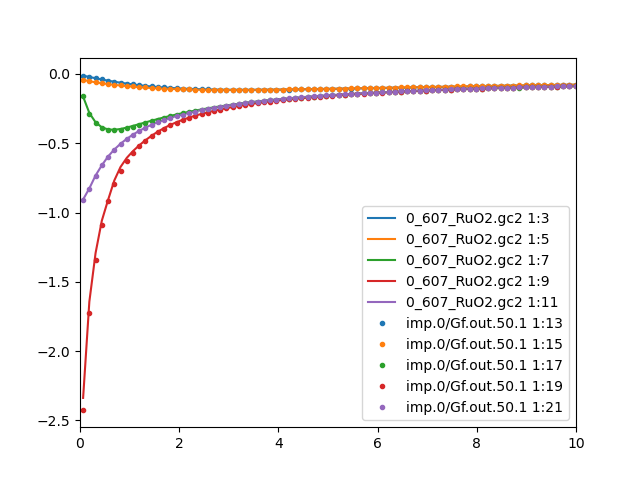
We now repeat previous steps to obtain the real axis spectra: 
saverage.py sig.inp.4[5-9] sig.inp.50
mkdir maxent
cd maxent
cp ../sig.inpx .
cp ../../oldrun/maxent/maxent_params.dat .
maxent_run.py sig.inpx
mkdir ../onreal
cd ../onreal
dmft_copy.py ../
cp ../../oldrun/onreal/0_607_RuO2.klist_band
x_lapw lapw0 -f 0_607_RuO2 
x_dmft.py lapw1 --band
x_dmft.py dmftp       
x_dmft.py dmftp -l dn
makplot.py 0.99
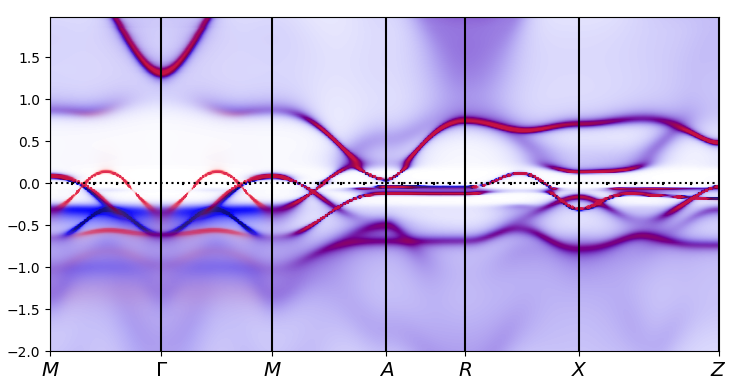
Finally we obtain the following spectral function:

Plotting 2D cuts of spectral function at EF

In this section we will plot the Fermi surface as a 2D cut in the BZ. This will show if the system has particular symmetry at the Gamma point, i.e., d-wave symmetry, for example. To do that, we first prepare input file "2D_params.py" in which we write 2D path we want to take in first BZ. The file can contain a single line, like: 
kpth = '[0.5*x,0.5*y,0]'
This means that we will make a cut at z=0. We choose the variable x to go from [-1,1], and variable y to also go from [-1,1]. Using these two variables, we define 2D plane in BZ for the 2D plot. We can execute 
bz.py
which will plot the first Brillouin zone and the 2D cut we choose to make.
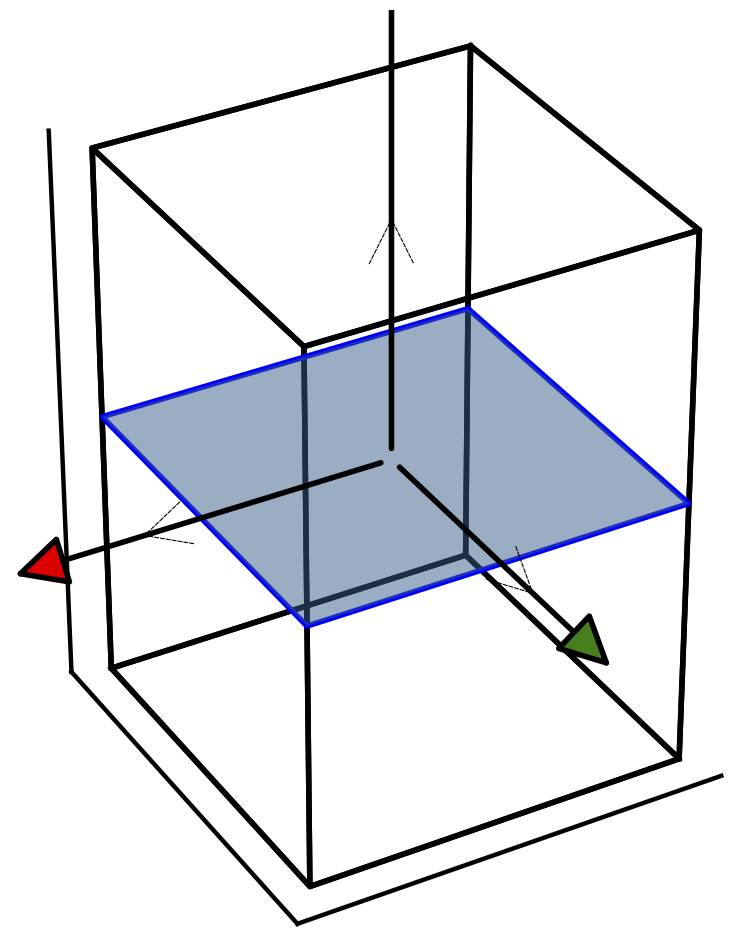The python script bz.py will produce the plot of the BZ. The blue plane shows the 2D cut we are making. The thick arrows are three reciprocal basis vectors, and the thin lines are chosen cartesian basis vectors. Note that the 2D plane in kpath=[] should be specified in cartesian basis, which is usually easier to comprehend than reciprocal basis. Note that the latter is in general non-orthogonal, while cartesian basis is always orthonormal. In this simple case the two basis coincide. Note also that red/gren/blue arrows stand for x/y/z direction. Next we execute 
2D_klist.py
which will produce "case.klist_band" that can be used to plot spectra. By default the number of k-points in single direction is "Nxy=90", which can be changed, if desired. Number of all k-points for this 2D plot is 91^2=8281. But when case.struct file contains all symmetry operations, this number can be reduced substantially. For example, RuO2 has 8 symmetry operations, and the non-equivalent momentum points are cut down to 2116. The output should say something like 
Number of all irreducible points= 2116 versus all= 8281
We want to plot only single frequency omega=0 to obtain the Fermi surface, hence we will slightly change "case.indmfl" file. The second line should be changed to 
0 0.025 0.025 2 0.0 0.01  # matsubara, broadening-corr, broadening-noncorr, nomega, omega_min, omega_max (in eV)
where nomega is set to 2, and frequency omega_min=0 and omega_max=0.01. This will actually produce a single frequency at the output (omega=0), but nomega=2 means that in addition to single point in infinity, we also have one extra point at zero frequency. Here we also assume that self-energy on the real axis is available in the current directory, and for example, density of states was computed prior. Than we recompute Kohn-Sham states, and DMFT eigenvalues by executing 
x_dmft.py lapw1 --band
x_dmft.py dmftp
x_dmft.py dmftp -l dn
This should produce "eigvals.dat" and "eigvalsdn.dat". These two files are text files that contain DFT+DMFT eigenvalues for up and down spins at specified zero frequency. Next we execute 
2D_kplot.py
to plot the Fermi surface on this cut.
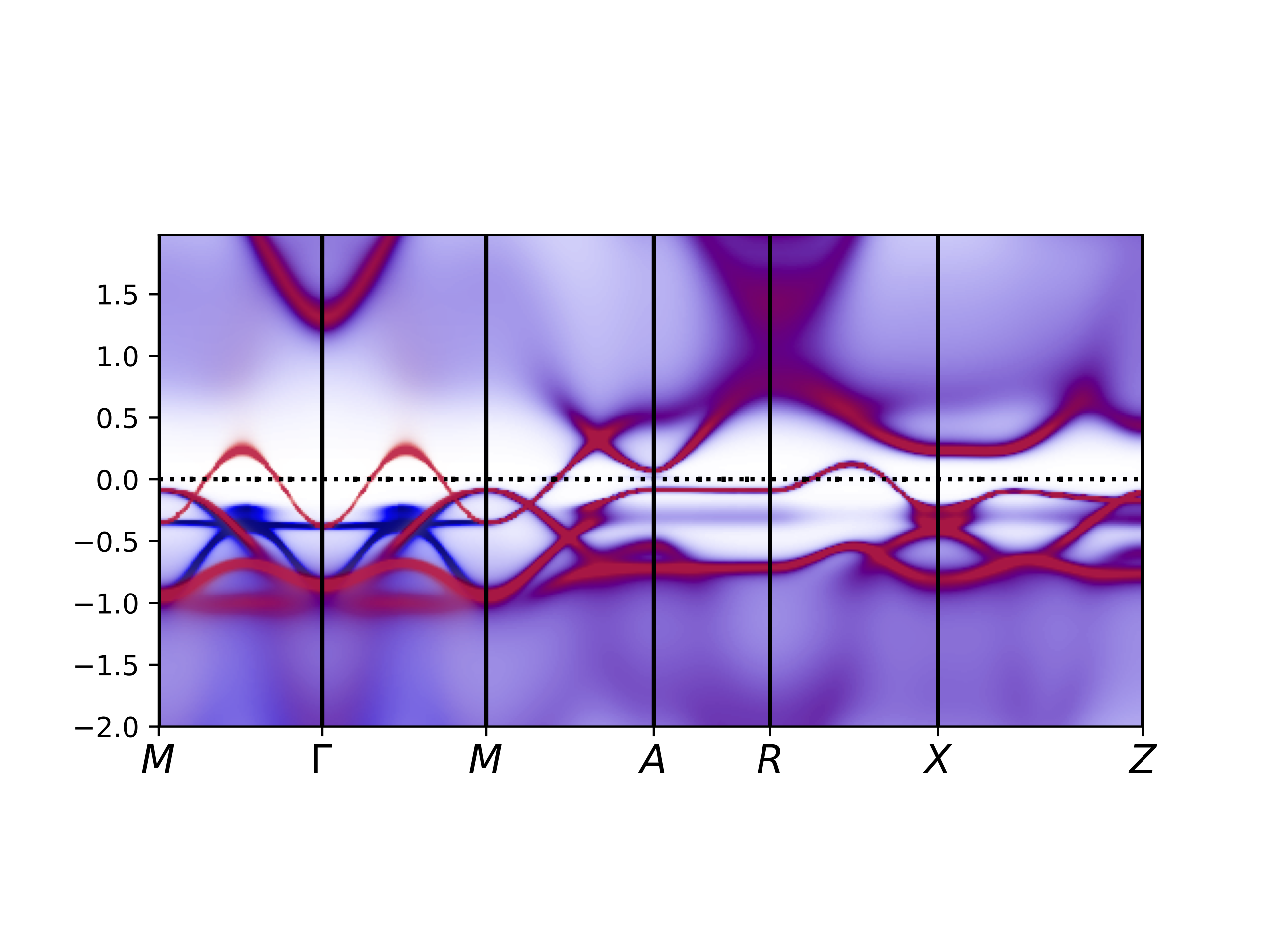
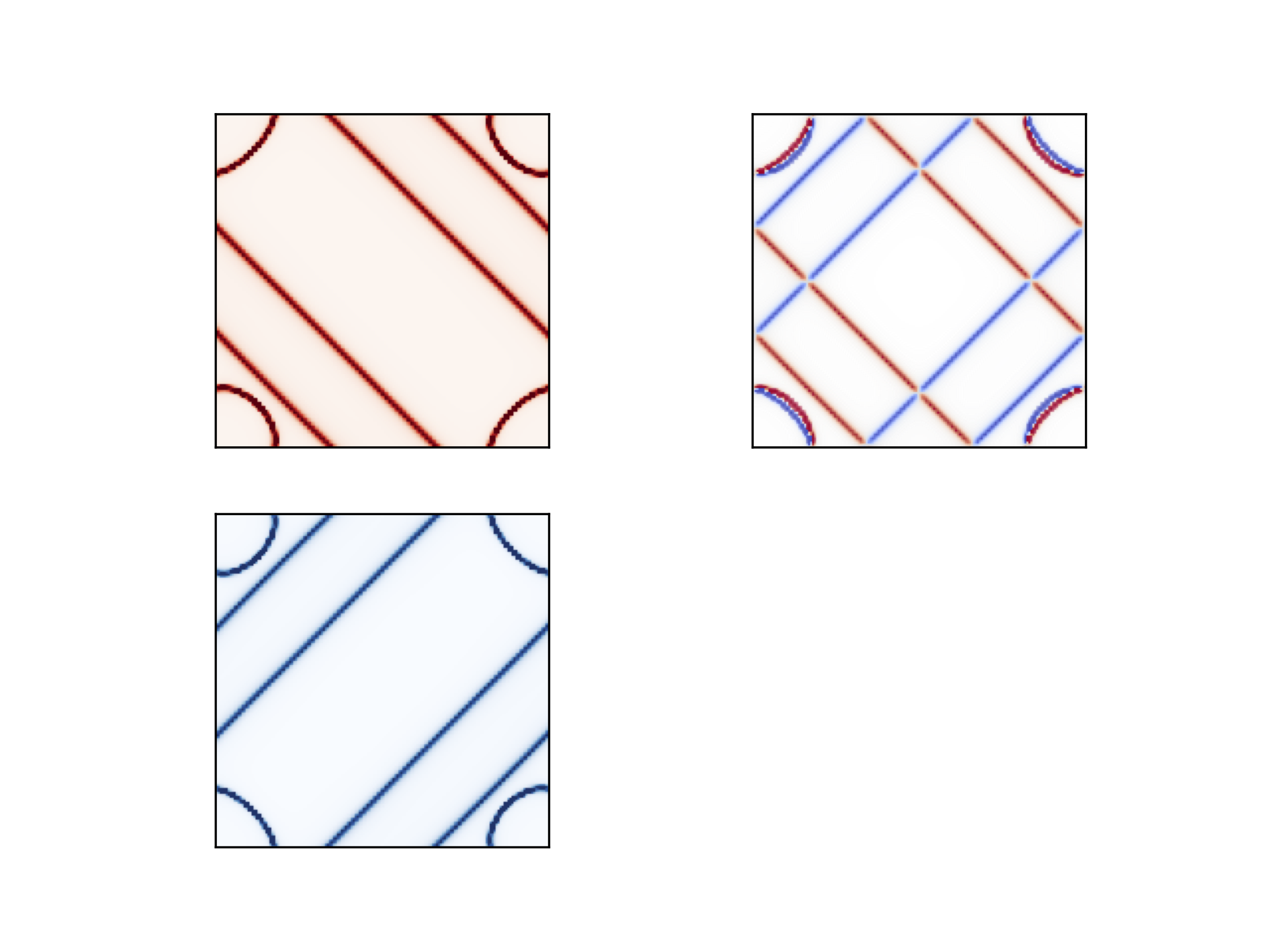On the left we see separately Fermi surface for up and down spins. On the right we see the combined plot with both spins present. Clearly the cut shows d-wave symmetry.
Last modified: Mon Aug 5 18:20:54 EDT 2024