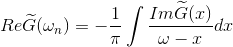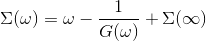Tutorial 1: MnO
Tutorial 1.a. : Preparing the input files
We begin by a simple example of a charge transfer insulator: MnO. It
cristalizes in the rock salt structure (two interpenetrating cubic FCC
str.) with lattice parameter
8.401155 a.u.. The Mn ion contains around 5 electrons, which
form the high spin state. The ground state has a large gap, which is
usually categorized as the charge transfer gap.
We will treat dynamically the Mn-d electrons.
The first step is to perform a DFT calculation to get a good
charge density. (We assume that the user has some familiarity with the
Wien2K code and we give only a very brief introductions to the DFT
part.)
First create a directory with the name MnO and copy the MnO.struct file into it. [Note that Wien2k requires to call directory
with the same name as the structure file].
The structure file contains the details of the crystal structure in the format
that Wien2K uses.
Note that the newest version of the code can work with
cif files, and can be initialized in much faster and simpler way with
cif2indmf.py script. You can learn more about that in
Docker Tutorial or Tutorial 9: High-throughput functionality.
To learn details of the eDMFT program flow, here we go though initialization step by step.
Initialize the DFT calculation by using
init_lapw
and then choosing the default options. In version 14, one needs to
type the following sequence of commands:
Enter reduction in %: 0
Use old or new scheme (o/N) : N
Do you want to accept these radii; .... (a/d/r) : a
specify nn-bondlength factor: 2
Ctrl-X-C
continue with sgroup : c
Ctrl-X-C
continue with symmetry : c
Ctrl-X-C
continue with lstart : c
specify switches for instgen_lapw (or press ENTER): ENTER
SELECT XCPOT: 13
SELECT ENERGY : -6
Ctrl-X-C
continue with kgen : c
Ctrl-X-C
Ctrl-X-C
NUMBER OF K-POINTS : 500
Ctrl-X-C
continue with dstart or execute kgen again or exit (c/e/x) : c
Ctrl-X-C
do you want to perform a spinpolarized calculation : n
Here Ctrl-X-C stands for breaking out of your editor. Ctrl-XC is used
in emacs and similar editors, but in vi, one should
replace Ctrl-X-C by :q!.
These are pretty much the default values that
Wien2K uses. We chose to work with the PBE functional (note that
total energies are better with LDA+DMFT functional, while spectra is
almost identical when using PBE or LDA), and use a
k-point grid of 500 points (in the whole Brillouin zone). Note
that spin-orbit interaction can be safely ignored as there are no
heavy ions in the system.
Note that instead of using the interactive way of determining
the DFT parameters, one can run wien2k initialization in batch mode,
by executing init_lapw with parameters:
init_lapw -b -vxc 13 -ecut -6.0 -rkmax 7 -numk 500
In version 24 of wien2k, the batch initialization is now default,
and only -m switch allows one to initialize manually.
Next, we can run the DFT calculation using the
command
run_lapw
In DMFT calculation, one needs converged
frequency dependent local Green's function, hence more k-points are
typically needed. We will increase the number of k-points to 2000
in this tutorial. To do that, run
x kgen
and specify 2000 k-points. Next, rerun wien2k on this k-mesh,
i.e., run_lapw -NI
(This step is not essential as the DFT charge
will not be very precise anyway for our DFT+Embedded-DMFT calculation).
Once the DFT calculation is done, we have a good charge
density to start a DMFT calculation. The next step is to initialize
the DMFT calculation. For this, we use the script
init_dmft.py.
Note that we can execute this python script interactively, or, with
giving parameters to the executable (batch mode).
Using faster batch mode, we might want to initialize dmft by
init_dmft.py -ca 1 -ot d -qs 7
The switch -ca specifies the correlated atom, -ot
specifies the orbital type, and -qs specifies the cubic
symmetry that we are going to use for this orbitals. These options
are explained below.
Alternatively, we might want to use the script
init_dmft.py in interactive mode, in which case we
just execute it, and answer the following questions:
Specify correlated atoms (ex: 1-4,7,8): 1
Do you want to continue; or edit again? (c/e): c
For each atom, specify correlated orbital(s) (ex: d,f):
1 Mn: d
Do you want to continue; or edit again? (c/e): c
Specify qsplit for each correlated orbital (default = 0):
1 Mn-1 d: 7
Do you want to continue; or edit again? (c/e): c
Specify projector type (default = 5): 5
Do you want to continue; or edit again? (c/e): c
Do you want to group any of these orbitals into cluster-DMFT problems? (y/n): n
Enter the correlated problems forming each unique correlated
problem, separated by spaces (ex: 1,3 2,4 5-8): 1
Do you want to continue; or edit again? (c/e): c
Range (in eV) of hybridization taken into account in impurity
problems; default -10.0, 10.0: <ENTER>
Perform calculation on real; or imaginary axis? (i/r) (default=i) : i
Ctrl-X-C
Is this a spin-orbit run? (y/n): n
Ctrl-X-C
Now we want to explain the options and their choice:
-
At the beginning, the code shows all atoms in the unit cell:
There are 2 atoms in the unit cell:
1 Mn
2 O
Specify correlated atoms (ex: 1-4,7,8): 1
and asks which one should be treated dynamically. We choose only the
first atom, Mn, to be treated as a correlated atom in the DMFT step.
- The code next asks which orbital quantum numbers should be
treated dynamically:
For each atom, specify correlated orbital(s) (ex: d,f):
1 Mn: d
The partially filled d shell of the Mn ion is to be treated in DMFT.
-
Next we should specify what type of local symmetry we have on the
given atom, and if we possibly want to correlated only a sub-shell
Specify qsplit for each correlated orbital (default = 0):
Qsplit Description
------ ------------------------------------------------------------
0 average GF, non-correlated
1 |j,mj> basis, no symmetry, except time reversal (-jz=jz)
-1 |j,mj> basis, no symmetry, not even time reversal (-jz=jz)
2 real harmonics basis, no symmetry, except spin (up=dn)
-2 real harmonics basis, no symmetry, not even spin (up=dn)
3 t2g orbitals
-3 eg orbitals
4 |j,mj>, only l-1/2 and l+1/2
5 axial symmetry in real harmonics
6 hexagonal symmetry in real harmonics
7 cubic symmetry in real harmonics
8 axial symmetry in real harmonics, up different than down
9 hexagonal symmetry in real harmonics, up different than down
10 cubic symmetry in real harmonics, up different then down
11 |j,mj> basis, non-zero off diagonal elements
12 real harmonics, non-zero off diagonal elements
13 J_eff=1/2 basis for 5d ions, non-magnetic with symmetry
14 J_eff=1/2 basis for 5d ions, no symmetry
------ ------------------------------------------------------------
1 Mn-1 d: 7
This chooses the local basis for the DMFT calculation. Notice that
current implementation of the DMFT in combination with CTQMC is basis
dependent. This is because by default we ignore off-diagonal
components of the hybridization function. (The code also supports
off-diagonal hybridization, but its use requires more advanced
options, and leads to a minus sign problem in the solution of the impurity.)
In MnO, we ignored the spin-orbit coupling, and
the crystal symmetry is cubic, hence hybridization is exactly
diagonal in the cubic harmonics basis. We thus want to use
this basis, which is the option 7. We could also use option 2, but
this would lead to a slight worse statistics as impurity solver now
averages over 3 t2g (or 2 eg) equivalent orbitals.
-
Specify projector type (default = 5):
Projector Drscription
------ ------------------------------------------------------------
1 projection to the solution of Dirac equation (to the head)
2 projection to the Dirac solution, its energy derivative,
LO orbital, as described by P2 in PRB 81, 195107 (2010)
4 similar to projector-2, but takes fixed number of bands in
some energy range, even when chemical potential and
MT-zero moves (folows band with certain index)
5 fixed projector, which is written to projectorw.dat. You can
generate projectorw.dat with the tool wavef.py
------ ------------------------------------------------------------
> 5
As discussed above, DMFT requires a local basis, i.e., projector to
local Green's function. If we could treat by DMFT all degrees of
freedom on a given atom, the solution would not depend on the choice
of the projector (it would depend on the range though). Fortunately,
the orbitals on Mn ion are quite nicely separated in energy, and the only
narrow states close to EF on Mn ion are the 3d states, hence they become
correlated. Note that the Mn 4s orbital is not far above EF, but the
4s state is very spatially extended, hence weakly correlated.
All choices of the projector project to spherical/cubic harmonics
inside a sphere around an atom, but the radial dependence of the
function is slightly different. "Projector 1" chooses solution of the
Dirac equation for the radial part, "Projector 2" chooses a
combination of the Dirac equation solution and its energy derivative,
"Projector 4" has the same radial component as Projector 2, but when
choosing an energy range for the projector, it will use equal number
of bands at each k-point (projector will follow bands). Finally,
projector 5 fixes the projector to the solution of the Dirac equation
on the LDA level.
If we are interested in the total free energy of the system, we should
use projector 5, because in this case the projector is fixed during
DMFT self-consistent run, which guarantees that the DFT+Embedded-DMFT method is
stationary.
- Cluster versus single-site DMFT option:
Do you want to group any of these orbitals into cluster-DMFT problems? (y/n): n
We do not attempt to do a cluster-DMFT calculation at this stage.
- For efficiency reasons, we want to solve impurity only for those
atoms which are different (and not related by symmetry). While we
could figure this out from the structure file, we allow the user to
set this here independently of the symmetry in the structure
file. This allows one to treat spontaneously broken states (such as
magnetically ordered states) in DMFT without reducing the crystal
symmetry.
Enter the correlated problems forming each unique correlated
problem, separated by spaces (ex: 1,3 2,4 5-8): 1
There is only one impurity in this system anyway.
- Choice for the energy range in the Kohn-Sham basis
Range (in eV) of hybridization taken into account in impurity
problems; default -10.0, 10.0:
This sets the energy range around the Fermi level, where the hybridizations
will be taken into account. Usually a value of the order of U is a good
starting guess, but one should check the resultant hybridization
to see that it is enough. "Projector 1" and "Projector 2" will
use all bands in this energy range. "Projector 4" and "5" will use the
same set of bands at each k-point, and to faithfully represent
the states in this energy range, it will automatically increase
the energy range in some k-points.
-
Perform calculation on real; or imaginary axis? (r/i): i
The CTQMC is an imaginary axis method.
-
Is this a spin-orbit run? (y/n): n
The spin-orbit coupling is ignored.
The init_dmft.py script generates two mandatory input files,
case.indmfl and case.indmfi, and also
projectorw.dat when fixed projector=5 is used. These
files connect the solid and the impurity with the DMFT engine, respectively.
Let us take a closer look at the header of the case.indmfl file:
5 15 1 5 # hybridization band index nemin and nemax, renormalize for interstitials, projection type
1 0.025 0.025 200 -3.000000 1.000000 # matsubara, broadening-corr, broadening-noncorr, nomega, omega_min, omega_max (in eV)
1 # number of correlated atoms
1 1 0 # iatom, nL, locrot
2 7 1 # L, qsplit, cix
The first line specifies the hybridization window. We set it to
"(-10eV,10eV)" around EF, which it turns out, contains bands numbered
from 5-15. For each k-point we will use the same bands, i.e., we will
follow the bands with the projector.
The same line also specified the projector type, which is 5.
The second line contains a switch for the real-axis or imaginary axis
calculation. If we require the local green's function or density of
states on real axis, we will set the switch "matsubara" to 0. Here, we
will work on imaginary axis, hence "matsubara" is set to 1.
The second line also contains information on small lorentzian broadening in
k-point summation. The last three numbers are used for plotting the
spectral functions, to which we will return latter.
The third line specifies the number of correlated atoms.
The forth line specifies which atom (from case.struct) is
correlated (Note that each atom in the structure file counts, even when
several atoms in structure files are equivalent). The forth line also
specifies how many orbital indeces (different L's) we will use for
projection, and calculation of local green's function and partial
dos. The last index "locrot" is used for rotation of local axis, and
is not needed here (set to 0).
The fifth line specifies orbital momentum "l=2", "qsplit=7" which we
chose during initialization. Each correlated orbital-set gets a
unique index during initialization. This correlated set was given index
"cix=1". For each correlated set, a more detailed specification is needed,
which is given in the remaining of "case.indmfl" file.
The specification of correlated set is given in the second part of case.indmfl:
#================ # Siginds and crystal-field transformations for correlated orbitals ================
1 5 2 # Number of independent kcix blocks, max dimension, max num-independent-components
1 5 2 # cix-num, dimension, num-independent-components
#---------------- # Independent components are --------------
'eg' 't2g'
#---------------- # Sigind follows --------------------------
1 0 0 0 0
0 1 0 0 0
0 0 2 0 0
0 0 0 2 0
0 0 0 0 2
#---------------- # Transformation matrix follows -----------
0.00000000 0.00000000 0.00000000 0.00000000 1.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
0.70710679 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.70710679 0.00000000
0.00000000 0.00000000 0.70710679 0.00000000 0.00000000 0.00000000 -0.70710679 0.00000000 0.00000000 0.00000000
0.00000000 0.00000000 0.00000000 0.70710679 0.00000000 0.00000000 0.00000000 0.70710679 0.00000000 0.00000000
-0.70710679 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.70710679 0.00000000
The first line specifies the number of all correlated blocks,
the dimension of the largest correlated block, and number of orbital
components which differ.
The second line specifies the dimension of the first correlated block
(here "d" has dimension 5), and the two eg and the three t2g components are treated
as degenerate.
The transformation matrix from spheric harmonics to the DMFT basis
is given in the end, and shows how these orbitals are defined:
It is the expansion of each of these orbitals in spherical
harmonics. The columns correspond to the following quantum numbers
(m_l=-2,-1,0,1,2) and rows to ('z^2','x^2-y^2','xz','yz','xy'). For
example, the 'z^2' orbital, which is expanded in the first line, is
equal to the m=0 spherical harmonic, whereas the yz orbital on the
forth line is an equal superposition of m=1 and m=-1, multiplied by i
(note that two consecutive real numbers define one complex
number).
Note that the transformation matrix must be unitary.
This file case.indmfl can be edited in text editor and can be adjusted if necessary.
The second file, created at the initialization, is case.indmfi and
contains the following lines:
1 # number of sigind blocks
5 # dimension of this sigind block
1 0 0 0 0
0 1 0 0 0
0 0 2 0 0
0 0 0 2 0
0 0 0 0 2
In this simplest case, where we have a single impurity problem, no new
information is contained in case.indmfi file, just the "Sigind" block
from case.indmfl is repeated. We will show more complex use of this
file later.
Now we want to start DMFT with the minimal number of necessary files.
To do this, create a new folder (with any name), and when in that folder, use the
command
dmft_copy.py <dft_results_directory>
where <dft_results_directory> is the directory where the
output of the DFT calculation with DMFT initialization is. This
command copies the necessary files to start a DMFT calculation. These
include the MnO.struct file as well as the various Wien2K input files
such as MnO.inm, MnO.in1, etc. The charge density file, MnO.clmsum, is also
copied. This is all we need from the initial Wien2K run, and now we
proceed to create the rest of the files, needed by the DMFT
calculation.
Copy the params.dat file.
This file contains information about the impurity solver and
additional parameteres, which appear in DFT+Embedded-DMFT. It is
written in Python format, and hence any Python syntax is accepted. For
checking the correct syntax, one can execute it as python script.
Its content is:
solver = 'CTQMC' # impurity solver
max_dmft_iterations = 1 # number of iteration of the dmft-loop only
max_lda_iterations = 100 # number of iteration of the LDA-loop only
finish = 10 # number of iterations of full charge loop (1 = no charge self-consistency).
# You should probably use 30 or so, but for testing 10 is OK.
ntail = 300 # on imaginary axis, number of points in the tail of the logarithmic mesh
cc = 5e-6 # the charge density precision to stop the LDA+DMFT run
ec = 5e-6 # the energy precision to stop the LDA+DMFT run
recomputeEF = 0 # Recompute EF in dmft2 step. If recomputeEF = 0, EF is fixed. Good for insulators.
DCs = 'exactd' # exact DC with dielectric model
wbroad = 0.0 # broadening of sigma on the imaginary axis
kbroad = 0.0 # broadening of sigma on the imaginary axis
# Impurity problem number 0
iparams0={"exe" : ["ctqmc" , "# Name of the executable"],
"U" : [9.0 , "# Coulomb repulsion (F0)"],
"J" : [1.14 , "# Coulomb J"],
"CoulombF" : ["'Ising'" , "# Density-density form. Can be changed to 'Full' "],
"beta" : [38.68 , "# Inverse temperature"],
"svd_lmax" : [25 , "# We will use SVD basis to expand G, with this cutoff"],
"M" : [5e6 , "# Total number of Monte Carlo steps per core"],
"mode" : ["SH" , "# We will use Greens function sampling, and Hubbard I tail"],
"nom" : [100 , "# Number of Matsubara frequency points sampled"],
"tsample" : [30 , "# How often to record measurements"],
"GlobalFlip" : [500000 , "# How often to try a global flip"],
"warmup" : [1e5 , "# Warmup number of QMC steps"],
"nf0" : [5.0 , "# Nominal valence we expect. Used only for starting DC."],
}
Note that this input file is a python script, and the correcteness of
its syntax can be
checked with Python interpreter by tying
python params.dat.
Below we explain the meaning of the variables
There is only one more file that we need: A blank self energy (sig.inp)
file. Generate it by the command
One can add parameters to the script, like
szero.py -e 38.22 -T 0.0258531540847983
Tutorial 1.b. : Submitting the job
Now we are ready to run DFT+Embedded-DMFT calculation. In
the simplest case, we can just run the script
However, single CPU will take a really long
time and the statistics will be too bad. One typically needs at least
100 cores (but more is better -- this jobs can easily scale to 100,000 cores) to achieve good statistics. [The DFT
part is most efficient when the number of cores is commensurate with
the number of k-points]. Note also
that the parameter "M" in params file specifies the number of Monte
Carlo steps per core, therefore more cores are available, better is
the result (but it is not faster in execution).
To submit a job to a parallel computer, we need to prepare a
submit script. This script must create a file "mpi_prefix.dat", which
contains the command for mpi parallel execution.
This command however depends very much on the operating
system and environment of a supercomputer.
On many systems, this command is called "mpirun", and in this case,
the submit script would contain
echo "mpirun -np $NSLOTS" > mpi_prefix.dat
where $NSLOTS stands for the number of available cores.
On some systems, the command might be:
echo "mpiexec -port $port -np $NSLOTS -machinefile $TMPDIR/machines" > mpi_prefix.dat
We can also tune the number of OpenMP threads per mpi node, which can
be achieved by giving an environmental variable OMP_NUM_THREADS
to mpi command. In
mpich, for example, one could set
echo "mpirun -np $NSLOTS -env OMP_NUM_THREADS 1" > mpi_prefix.dat
echo "mpirun -np $NSLOTS -x OMP_NUM_THREADS=1" > mpi_prefix.dat
Finally, once we created "mpi_prefix.dat" file, we should run the DFT+Embedded-DMFT script by
$WIEN_DMFT_ROOT/run_dmft.py > nohup.dat 2>&1
Note that the python script is not run with mpi. However, the impurity
solver, and other dmft steps will be executed in parallel using
command specified in "mpi_prefix.dat".
As discussed above, if many more CPU-cores are available than the number of k-points, we can
optimize the execution further. Namely, a single k-point can be
executed on many cores using OpenMP instructions. To use this
feature, one needs to specify "mpi_prefix.dat2" in addition to
"mpi_prefix.dat" file. The former is than used in the dft part of the
loop, while the latter is used by the impurity solver.
Clearly, "mpi_prefix.dat2" should specify the mpi command, which is started
on a subset of machines. Therefore "-np" should be smaller than
"$NSLOTS" and "OMP_NUM_THREADS" should be larger than 1.
Before submitting the job, make sure that the computing notes have the
following environmental
variable specified: $WIENROOT, $WIEN_DMFT_ROOT, $SCRATCH.
If lapw1 and lapwso are executed through
x_dmft.py script, then these variables need to be set only on
the master node. Otherwise all compute nodes need to have these
variables set.
Also make sure that $WIEN_DMFT_ROOT is in $PYTHONPATH on the master node.
It is advisable to add $WIENROOT and $WIEN_DMFT_ROOT to the $PATH,
although it is not mandatory.
Typically, the .bashrc (or its equivalent) should contain
the following lines:
export WIENROOT=<wien-instalation-dir>
export WIEN_DMFT_ROOT=<dir-containing-dmft-executables>
export SCRATCH="."
export PATH=$PATH:$WIENROOT:$WIEN_DMFT_ROOT
export PYTHONPATH=$PYTHONPATH:$WIEN_DMFT_ROOT
Note that SCRATCH does not need to point to the current directory,
instead it could be more efficient to have it set to SCRATCH=/tmp/ or
SCRATCH=/scratch/, so that the large vector files are written locally
for each process.
It might be necessary to repeat these commands (seeting variables)
also in the submit script. This of ocurse depends on the system.
Here we paste an example of the submit script for SUN Grid Engine
, but different system will require different script.
#!/bin/bash
set -x
########################################################################
# SUN Grid Engine job wrapper
# parallel job on opteron queue
########################################################################
#$ -N MnO
#$ -pe orte 100
#$ -q <your_queue>
#$ -j y
#$ -M <email@your_institution>
#$ -m e
#$ -v WIEN_DMFT_ROOT,WIENROOT,LD_LIBRARY_PATH,PATH
########################################################################
source $TMPDIR/sge_init.sh
########################################################################
export SMPD_OPTION_NO_DYNAMIC_HOSTS=1
export MODULEPATH=/opt/apps/modulefiles:/opt/intel/modulefiles:/opt/gnu/modulefiles:/opt/sw/modulefiles
export SCRATCH="."
export OMP_NUM_THREADS=1
export PATH=.:$PATH
module load iompi/wien/19
module load intel/2024
module load intel/ompi
export WIEN_DMFT_ROOT=<path_to_executable>
export LD_LIBRARY_PATH=/opt/intel/24.0/ompi/arpack/lib:/opt/intel/24.0/ompi/fftw-3.3.10-mpi/lib:/opt/intel/24.0/ompi/lib:/opt/intel/oneapi/2024.0/lib
# scp -r rupc-01:$SGE_O_WORKDIR/ $WORK/$jobdir/
echo "mpirun -n $NSLOTS" > mpi_prefix.dat
echo "mpirun -n $NSLOTS" > mpi_prefix.dat2
$WIEN_DMFT_ROOT/run_dmft.py >& nohup.dat
#!/bin/bash
#PBS -l walltime=12:00:00,nodes=72:ppn=16
#PBS -N MnO
#PBS -j oe
export WIENROOT=<your_w2k_root>
export WIEN_DMFT_ROOT=<your_dmft_root>
export PYTHONPATH=$PYTHONPATH:.:$WIEN_DMFT_ROOT
export SCRATCH='.'
cd $PBS_O_WORKDIR
echo "mpirun -np 1152 -x OMP_NUM_THREADS=1" > mpi_prefix.dat
echo "mpirun -np 72 -x OMP_NUM_THREADS=16" > mpi_prefix.dat2
$WIEN_DMFT_ROOT/run_dmft.py >& nohup.dat
rm -f $JOBNAME.vector*
Tutorial 1.c. : Monitoring the job
While the code is running, there are multiple files that you can check
to see how it is going. One is the ':log' file, which serves exactly
the same purpose as in Wien2K. It lists the individual
modules that are run:
Thu Mar 23 22:57:43 EDT 2017> (x) -f MnO lapw0
Thu Mar 23 22:57:45 EDT 2017> lapw1
Thu Mar 23 22:57:46 EDT 2017> dmft1
Thu Mar 23 22:57:47 EDT 2017> impurity
Thu Mar 23 23:00:13 EDT 2017> dmft2
Thu Mar 23 23:00:14 EDT 2017> (x) -f MnO lcore
Thu Mar 23 23:00:15 EDT 2017> (x) -f MnO mixer
Thu Mar 23 23:00:16 EDT 2017> (x) -f MnO lapw0
Thu Mar 23 23:00:37 EDT 2017> lapw1
Thu Mar 23 23:00:38 EDT 2017> dmft2
Thu Mar 23 23:00:41 EDT 2017> (x) -f MnO lcore
Thu Mar 23 23:00:41 EDT 2017> (x) -f MnO mixer
Thu Mar 23 23:00:43 EDT 2017> (x) -f MnO lapw0
Thu Mar 23 23:00:45 EDT 2017> lapw1
Thu Mar 23 23:00:47 EDT 2017> dmft2
Thu Mar 23 23:00:48 EDT 2017> (x) -f MnO lcore
Thu Mar 23 23:00:51 EDT 2017> (x) -f MnO mixer
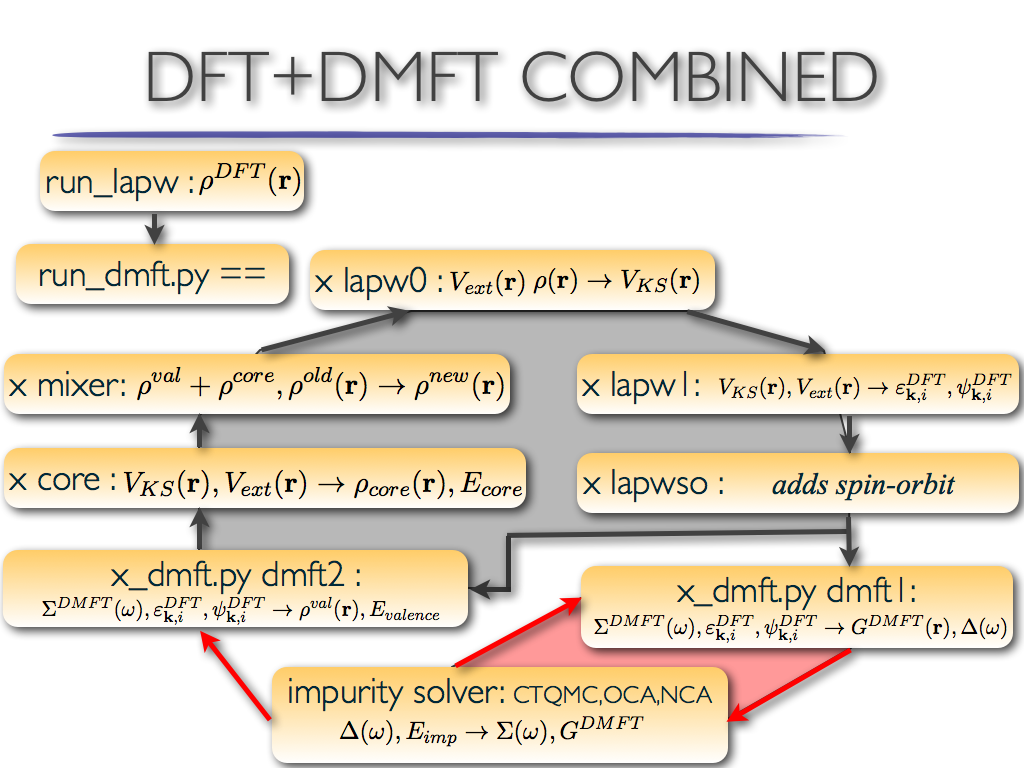
The code starts by running the lapw0 and lapw1 modules of Wien2K to
calculate the vector files, etc; but then, dmft1 and dmft2 steps are
inserted. Impurity is running in-between dmft1 and dmft2
step. The dmft2 step replaces the lapw2 step of Wien2k.
Since DFT part is here very fast (much faster than impurity solver),
we used several DFT step (up to 100) in combination with a single dmft
step. Therefore after dmft1, one can see several blocks of the
following cycle repeated: dmft2,lcore,mixer,lapw0,lapw1. This is the
charge loop. The reason to do this is to obtain a well converged DFT
run between each dmft1 step, since dmft1 is the most time consuming
part (as can be seen in the timing information above). Whether the
charge density is well converged can be checked by grep'ing ':CHARGE'
in the .dayfile:
grep ':CHARGE' MnO.dayfile
:CHARGE convergence: 0.3650051
:CHARGE convergence: 0.320649
:CHARGE convergence: 0.1980197
:CHARGE convergence: 0.1882957
:CHARGE convergence: 0.1454709
:CHARGE convergence: 0.0432447
:CHARGE convergence: 0.0190978
:CHARGE convergence: 0.0055925
:CHARGE convergence: 0.0048235
:CHARGE convergence: 0.0024782
:CHARGE convergence: 0.0006552
:CHARGE convergence: 0.0001947
:CHARGE convergence: 0.0002805
:CHARGE convergence: 2.05e-05
:CHARGE convergence: 1.16e-05
:CHARGE convergence: 1.69e-05
:CHARGE convergence: 1.84e-05
:CHARGE convergence: 1.4e-06
Note that the charge converges at fixed self-energy, but when
the self-energy is updated (after dmft1 step) the charge is again
non-converged.
Towards the end of the run (after
about 20 cycles), the self enery is also converged and so the jump in
the charge after each dmft1
is much less significant:
0 :CHARGE convergence: 0.3650051
1 :CHARGE convergence: 0.320649
2 :CHARGE convergence: 0.1980197
3 :CHARGE convergence: 0.1882957
4 :CHARGE convergence: 0.1454709
5 :CHARGE convergence: 0.0432447
6 :CHARGE convergence: 0.0190978
7 :CHARGE convergence: 0.0055925
8 :CHARGE convergence: 0.0048235
9 :CHARGE convergence: 0.0024782
10 :CHARGE convergence: 0.0006552
11 :CHARGE convergence: 0.0001947
12 :CHARGE convergence: 0.0002805
13 :CHARGE convergence: 2.05e-05
14 :CHARGE convergence: 1.16e-05
15 :CHARGE convergence: 1.69e-05
16 :CHARGE convergence: 1.84e-05
17 :CHARGE convergence: 1.4e-06
....
....
51 :CHARGE convergence: 0.0046878
52 :CHARGE convergence: 0.0041113
53 :CHARGE convergence: 0.00243
54 :CHARGE convergence: 0.0013541
55 :CHARGE convergence: 0.0006717
56 :CHARGE convergence: 0.000342
57 :CHARGE convergence: 0.0001287
58 :CHARGE convergence: 3.47e-05
59 :CHARGE convergence: 1.37e-05
60 :CHARGE convergence: 3.6e-06
61 :CHARGE convergence: 0.002555
62 :CHARGE convergence: 0.0022443
63 :CHARGE convergence: 0.0013392
64 :CHARGE convergence: 0.0007663
65 :CHARGE convergence: 0.0003645
66 :CHARGE convergence: 0.0002563
67 :CHARGE convergence: 7.28e-05
68 :CHARGE convergence: 1.09e-05
69 :CHARGE convergence: 9.6e-06
70 :CHARGE convergence: 6.1e-06
71 :CHARGE convergence: 6e-07
....
....
135 :CHARGE convergence: 0.0002954
136 :CHARGE convergence: 0.0002592
137 :CHARGE convergence: 0.0001538
138 :CHARGE convergence: 0.0001346
139 :CHARGE convergence: 5.24e-05
140 :CHARGE convergence: 2.72e-05
141 :CHARGE convergence: 6.8e-06
142 :CHARGE convergence: 3.2e-06
143 :CHARGE convergence: 0.0003925
144 :CHARGE convergence: 0.0003348
145 :CHARGE convergence: 0.0001878
146 :CHARGE convergence: 0.0001563
147 :CHARGE convergence: 4.16e-05
148 :CHARGE convergence: 2.61e-05
149 :CHARGE convergence: 1.05e-05
150 :CHARGE convergence: 2.8e-06
Another important file to check is the info.iterate, which contains
information about the chemical potential, the number of electrons on
the V ion, etc:
# #. # mu Vdc Etot Ftot+T*Simp Ftot+T*Simp n_latt n_imp Eimp[0] Eimp[-1]
0 0. 0 6.531263 37.772879 -2467.797924 -2467.812926 -2467.796784 4.832377 5.013534 0.054065 -0.045105
1 0. 1 6.531263 37.772879 -2467.795198 -2467.839362 -2467.794737 4.856478 5.013534 0.054065 -0.045105
2 0. 2 6.531263 37.772879 -2467.790068 -2467.919012 -2467.791341 4.928763 5.013534 0.054065 -0.045105
3 0. 3 6.531263 37.772879 -2467.805037 -2468.148462 -2467.807211 5.119680 5.013534 0.054065 -0.045105
4 0. 4 6.531263 37.772879 -2467.806312 -2468.041367 -2467.803524 4.975357 5.013534 0.054065 -0.045105
5 0. 5 6.531263 37.772879 -2467.797455 -2468.058270 -2467.797604 4.989835 5.013534 0.054065 -0.045105
6 0. 6 6.531263 37.772879 -2467.795467 -2468.037324 -2467.795559 4.964081 5.013534 0.054065 -0.045105
7 0. 7 6.531263 37.772879 -2467.795670 -2468.039345 -2467.795727 4.967218 5.013534 0.054065 -0.045105
8 0. 8 6.531263 37.772879 -2467.795453 -2468.037709 -2467.795553 4.968465 5.013534 0.054065 -0.045105
9 0. 9 6.531263 37.772879 -2467.795395 -2468.034744 -2467.795412 4.970982 5.013534 0.054065 -0.045105
10 0. 10 6.531263 37.772879 -2467.794961 -2468.029487 -2467.794965 4.974418 5.013534 0.054065 -0.045105
11 0. 11 6.531263 37.772879 -2467.794815 -2468.027650 -2467.794804 4.974379 5.013534 0.054065 -0.045105
12 0. 12 6.531263 37.772879 -2467.794816 -2468.027676 -2467.794805 4.974472 5.013534 0.054065 -0.045105
13 0. 13 6.531263 37.772879 -2467.794813 -2468.027656 -2467.794803 4.974440 5.013534 0.054065 -0.045105
14 0. 14 6.531263 37.772879 -2467.794813 -2468.027658 -2467.794803 4.974441 5.013534 0.054065 -0.045105
15 0. 15 6.531263 37.772879 -2467.794813 -2468.027657 -2467.794803 4.974440 5.013534 0.054065 -0.045105
16 0. 16 6.531263 37.772879 -2467.794813 -2468.027655 -2467.794803 4.974440 5.013534 0.054065 -0.045105
17 1. 0 6.531263 37.940316 -2467.791665 -2467.796323 -2467.793875 5.101315 5.033536 -0.240213 -0.362603
18 1. 1 6.531263 37.940316 -2467.791016 -2467.781532 -2467.792627 5.089714 5.033536 -0.240213 -0.362603
19 1. 2 6.531263 37.940316 -2467.789431 -2467.737004 -2467.789185 5.054946 5.033536 -0.240213 -0.362603
20 1. 3 6.531263 37.940316 -2467.787966 -2467.669527 -2467.784865 5.006160 5.033536 -0.240213 -0.362603
21 1. 4 6.531263 37.940316 -2467.786916 -2467.648442 -2467.783808 5.018529 5.033536 -0.240213 -0.362603
22 1. 5 6.531263 37.940316 -2467.785769 -2467.646216 -2467.783363 5.028555 5.033536 -0.240213 -0.362603
23 1. 6 6.531263 37.940316 -2467.785657 -2467.641236 -2467.783057 5.024862 5.033536 -0.240213 -0.362603
24 1. 7 6.531263 37.940316 -2467.785486 -2467.638166 -2467.782886 5.025596 5.033536 -0.240213 -0.362603
25 1. 8 6.531263 37.940316 -2467.785492 -2467.638303 -2467.782892 5.025582 5.033536 -0.240213 -0.362603
26 1. 9 6.531263 37.940316 -2467.785489 -2467.638261 -2467.782888 5.025539 5.033536 -0.240213 -0.362603
27 1. 10 6.531263 37.940316 -2467.785488 -2467.638250 -2467.782887 5.025538 5.033536 -0.240213 -0.362603
28 1. 11 6.531263 37.940316 -2467.785489 -2467.638264 -2467.782888 5.025541 5.033536 -0.240213 -0.362603
29 2. 0 6.531263 37.919732 -2467.784434 -2467.789381 -2467.784203 5.024368 5.031140 -0.077242 -0.205319
30 2. 1 6.531263 37.919732 -2467.784453 -2467.790595 -2467.784272 5.025296 5.031140 -0.077242 -0.205319
31 2. 2 6.531263 37.919732 -2467.784511 -2467.794236 -2467.784480 5.028077 5.031140 -0.077242 -0.205319
....
....
153 14. 6 6.531263 37.919319 -2467.784809 -2467.786146 -2467.784766 5.031462 5.031090 -0.090639 -0.218392
154 14. 7 6.531263 37.919319 -2467.784806 -2467.786104 -2467.784764 5.031478 5.031090 -0.090639 -0.218392
155 14. 8 6.531263 37.919319 -2467.784806 -2467.786091 -2467.784763 5.031482 5.031090 -0.090639 -0.218392
156 14. 9 6.531263 37.919319 -2467.784805 -2467.786087 -2467.784763 5.031482 5.031090 -0.090639 -0.218392
157 15. 0 6.531263 37.917886 -2467.784779 -2467.789688 -2467.784788 5.031145 5.030921 -0.085861 -0.213710
158 15. 1 6.531263 37.917886 -2467.784780 -2467.789750 -2467.784791 5.031194 5.030921 -0.085861 -0.213710
159 15. 2 6.531263 37.917886 -2467.784784 -2467.789936 -2467.784802 5.031343 5.030921 -0.085861 -0.213710
160 15. 3 6.531263 37.917886 -2467.784789 -2467.790227 -2467.784820 5.031569 5.030921 -0.085861 -0.213710
161 15. 4 6.531263 37.917886 -2467.784792 -2467.790226 -2467.784820 5.031496 5.030921 -0.085861 -0.213710
162 15. 5 6.531263 37.917886 -2467.784793 -2467.790225 -2467.784820 5.031493 5.030921 -0.085861 -0.213710
163 15. 6 6.531263 37.917886 -2467.784793 -2467.790227 -2467.784821 5.031488 5.030921 -0.085861 -0.213710
164 15. 7 6.531263 37.917886 -2467.784794 -2467.790230 -2467.784821 5.031487 5.030921 -0.085861 -0.213710
The second column counts the number of DMFT steps (impurity solver),
the third counts charge steps at each DMFT steps, next columns shows
the chemical potential, the fifth column shows the double-counting
potential, the sixth column shows total energy, followed by two
different estimates of the free energy. The seventh column estimate of
the free energy is not precise, instead the eight column should be
used. [Notice that all quantities, except the total energy and
the free energy are give in eV. The total energies and free energies
are give in Ry, to be compatible with wien2k].
The ninth and tenth column show the impurity occupation
computed from the solid (n_latt) and from the impurity (n_imp).
The last two columns show the impurity levels.
The chemical potential in this insulating materials is fixed. The impurity occupation,
computed from the solid, is quite off at the beginning, however, it becomes
close to nominal 5.0 is just a few iterations. When the calculation is
converged, n_latt and n_imp should match.
Very many steps appear in info.iterate file, and sometimes we
just want to print one line per each dmft steps (the step at which the
charge is converged, and just before the self-energy is updated). This would correspond to step
16,28,... in the above example.
We can execute
to list only these dmft steps. We can then plot the lattice and
impurity occupation, which should look like this:
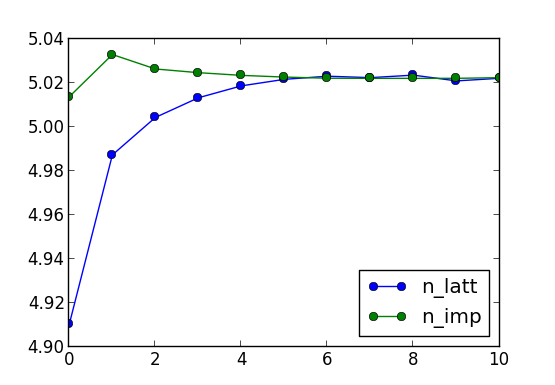 Within 6 dmft iterations, the charge is converged to 5.032, and we can
now increase the precision of the Monte Carlo steps. For example,
increase M in params.dat file for factor of 4-5 to have
much more precise statistics in the last few iterations.
Within 6 dmft iterations, the charge is converged to 5.032, and we can
now increase the precision of the Monte Carlo steps. For example,
increase M in params.dat file for factor of 4-5 to have
much more precise statistics in the last few iterations.
Notice that each variable in params.dat file can be
changed during the run, and it will be updated during the run.
Within 10 or so dmft iterations (around 120 charge iterations), the total energy and the free energy are
converged within 1meV (using 216 cores for impurity solver), as seen here:
 Notice that total energy (or free energy) would converge better only
if Monte Carlo statistics is increase, as resulting noise is due to MC noise.
Notice that total energy (or free energy) would converge better only
if Monte Carlo statistics is increase, as resulting noise is due to MC noise.
Other files to monitor the run include
dmft_info.out -- prints what is being executed, and what were parameters
MnO.scf -- like in dft, contains energies and forces and lots of other info
dmft1_info.out -- progress of dmft1 step
MnO.outputdmf1 -- log file of the dmft1 step. Contains the density matrix in :NCOR and the matrix of impurity levels.
dmft2_info.out -- progress of dmft2 step
MnO.outputdmf2 -- log file of the dmft2 step (similar to MnO.output2 from lapw2); contains energies and forces.
MnO.dlt1* -- the hybridization function
MnO.gc1* -- the local green's function
imp.0/ctqmc.log* -- log file of the impurity solver
imp.0/nohup_imp.out.xxx -- progress of the impurity solver for each mpi process
Delta.inp* -- input hybridization function
imp.0/histogram.dat -- the histogram of the perturbation order, i.e., how many kinks does the time evolution contain
Even though the impurity occupations and total energy
converged, we should check the spectral functions to decide if the run
is properly converged. In a metal, it is best to look at the
self-energy (impurity self-energies are at : imp.0/Sig.out*,
while the lattice self-energy, which is just a combination of impurity
ones, are at: sig.inp*).
In a Mott insulator, the self-energy on real axis has a pole inside the gap, and
therefore its shape on imaginary axis is very sensitive to the relative position of the
chemical potential an the pole. If one accidentally hits the pole by
placing mu on it, the self-energy on imaginary axis diverges at zero frequency. If
however the chemical potential is slightly moved away from the pole,
self-energy just becomes large at finite frequencies, but its
imaginary part vanishes at zero. This is because on real axis the imaginary part
vanishes inside the gap, except for the pole. The real part is large,
but not diverging, except when chemical potential is at the pole. The
shape of the self-energy on imaginary axis is therefore not very
illustrative.
We will therefore rather concentrate on the Green's function, of which
the imaginary part needs to vanish at zero frequency (both on the real and
the imaginary axis). Here is the plot of the impurity Green's function
with iterations:
 We see that the green's function is metallic only at the first
iteration, while at the second iteration is almost converged. Such
rapid convergence is here due to the robustness of the gap in the
high-spin state on Mn.
We see that the green's function is metallic only at the first
iteration, while at the second iteration is almost converged. Such
rapid convergence is here due to the robustness of the gap in the
high-spin state on Mn.
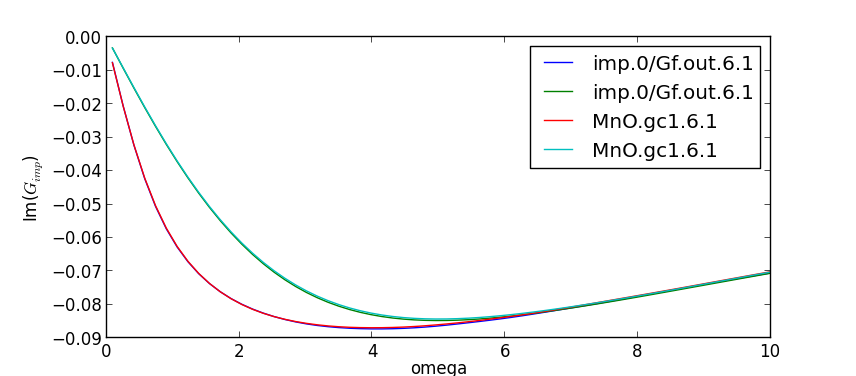
We should always check that the impurity and the local green's
function of the solid match. This is a very non-trivial check of the
correctness of the calculation, as the algorithm equates only the
self-energy at each iteration, while the Green's functions differ
until the self-consistency is achieved. We see that at the six-th
dmft iteration, the two Green's functions match very well:
 Notice that the last Green's functions are named imp.0/Gf.out
and MnO.gc1, while each previous iteration is saved under the
same name, with consecutive number attached to it. The first number
stands for the number of the outside loop, while the second number
enumerates the steps inside the dmft loop (red loop in the figure
above). Since we have max_dmft_iterations=1, the second number
is always 1. The first number would go from 1 to the parameter
finish from params.dat file, or less, if the convergence is
achieved earlier
Notice that the last Green's functions are named imp.0/Gf.out
and MnO.gc1, while each previous iteration is saved under the
same name, with consecutive number attached to it. The first number
stands for the number of the outside loop, while the second number
enumerates the steps inside the dmft loop (red loop in the figure
above). Since we have max_dmft_iterations=1, the second number
is always 1. The first number would go from 1 to the parameter
finish from params.dat file, or less, if the convergence is
achieved earlier
We see that for practical purposes, the convergence is achieved around
6-7th iteration, and the next steps are within the statistical noise
identical. The job would not finish though, because by default (to be
cautious) the convergence criteria are set very high. It is therefore
desirable to kill the job, once the overal convergence is obviously
achieved.
Tutorial 1.d. : Postprocessing, analytic continuation, DOS
At this point, we can proceed to the next step of plotting spectra on
the real axis.
Once the calculation is done on the imaginary axis, we need
to do analytical continuation to obtain the self energy on the real
axis. For this, we first take average of the sig.inp files from the
last few steps (in order to reduce the noise) by
saverage.py sig.inp.1[0-5].1
The output is written to sig.inpx. We could append -o
option, if we wanted to change this name.
All python scripts include a short help, so by executing for example
it prints the options for this script.
Next, create a new directory (lets call it maxent), and copy the averaged self energy
sig.inpx into it. Also copy
the maxent_params.dat file,
which contains the parameters for the analytical continuation
process:
params={'statistics': 'fermi', # fermi/bose
'Ntau' : 300, # Number of time points
'L' : 20.0, # cutoff frequency on real axis
'x0' : 0.005, # low energy cut-off
'bwdth' : 0.004, # smoothing width
'Nw' : 300, # number of frequency points on real axis
'gwidth' : 2*15.0, # width of gaussian
'idg' : 1, # error scheme: idg=1 -> sigma=deltag ; idg=0 -> sigma=deltag*G(tau)
'deltag' : 0.004, # error
'Asteps' : 4000, # anealing steps
'alpha0' : 1000, # starting alpha
'min_ratio' : 0.001, # condition to finish, what should be the ratio
'iflat' : 1, # iflat=0 : constant model, iflat=1 : gaussian of width gwidth, iflat=2 : input using file model$
'Nitt' : 1000, # maximum number of outside iterations
'Nr' : 0, # number of smoothing runs
'Nf' : 40, # to perform inverse Fourier, high frequency limit is computed from the last Nf points
}
Perhaps the most important is mesh on the real axis, which is given by
the upper cutoff L, the low energy cutoff x0 and
Nw points. The mesh is non-uniform and more dense at low energy
(tan-mesh).
The MC error is here set to 0.004, and can be estimated from the
variation in sig.inp.? files. Notice that we do not continue
the self-energy, which would have very large error, and would not be
stable to continue analytically. We will analytically continue an auxiliary
function, which is constructed as

and then perform Kramers-Kronig on imaginary part of this function:
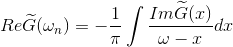
and finally invert it to solve for the self-energy on the real
axis
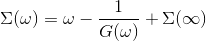
The script which does that is called maxent_run.py. We
will thus run
which uses the
maximum entropy method to do analytical continuation. This creates the
self energy Sig.out on the real axis. It should be similar to this plot:
 Notice that both orbitals have Mott-type gap, as there is a pole in
the gap. The sizes of the two gaps are different, with the eg orbitals
having somewhat larger (4.8eV) and t2g smaller (2.7eV) gap.
Notice that both orbitals have Mott-type gap, as there is a pole in
the gap. The sizes of the two gaps are different, with the eg orbitals
having somewhat larger (4.8eV) and t2g smaller (2.7eV) gap.
Now we need to make one last dmft1 calculation in order to obtain the
Green's function and DOS on the real axis. Create a new directory
inside your output directory, and while it the new directory, use
to copy necessary files from the output of the DMFT run to the new directory. Also copy the
analytically continued self energy Sig.out to sig.inp in this new
directory:
cp ../maxent/Sig.out sig.inp
Since we need to run the code on the real axis, we need to
change the NiO.indmfl file. The first number on the second line
of NiO.indmfl file determines whether the code is run on the real axis (0) or the
imaginary axis (1). Change it to 0. The header of MnO.indmfl
file should now look like
5 15 1 5 # hybridization band index nemin and nemax, renormalize for interstitials, projection type
0 0.025 0.025 200 -3.000000 1.000000 # matsubara, broadening-corr, broadening-noncorr, nomega, omega_min, omega_max (in eV)
1 # number of correlated atoms
1 1 0 # iatom, nL, locrot
2 7 1 # L, qsplit, cix
Then, inside the new directory run
x lapw0 -f MnO
x_dmft.py lapw1
x_dmft.py dmft1
-f MnO specifies that name of the
wien2k-files (called case) is different than the
directory name. Namely, in wien2k it is mandatory to use directory
name with the same base-name than structure file and all other files that
are being produced. In eDMFT we don't require that, and when directory
name is different than case, but we call
original wien2k commands, we need to use -f option to
circumvent the wien2k restriction.
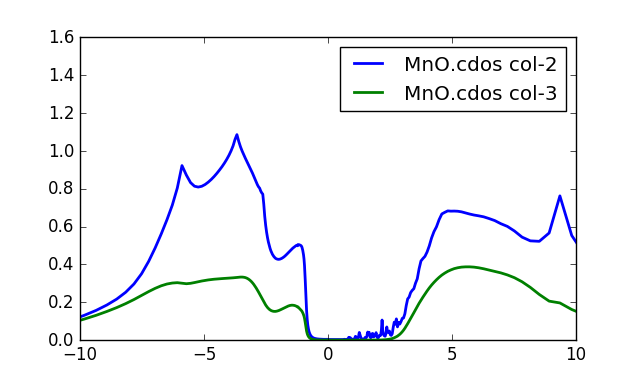
Once the run is done, we now have the densities of states on
the real axis. Both the total (column 2) and partial Mn-d (column 3)
are stored in MnO.cdos:
 To obtain this plot, we increased the number of k-points to
10,000. The procedure is the same as above: rerun
To obtain this plot, we increased the number of k-points to
10,000. The procedure is the same as above: rerun x kgen -f MnO
and when asked enter 10000. Then rerun lapw1 and dmft1
step.
Notice that the first excitation into the valence band has roughly
1/3 of d-character, and 2/3 of the oxygen character. Notice also that
this is not the real lower Hubbard band within our description, as U
is too large (9eV). This peak is than due to screening of the Mn large
spin by oxygen degrees of freedom, and is a type of Kondo effect. It
is interesting to point out that even in an insulator the Kondo effect
is not completely absent, as such screening occurs at the first
possible excitation. In literature, such effect is also called
Zhang-Rice singlet, as it was first discussed in cuprates by Zhang & Rice.
Lets note that the first excitation into the conduction band is of
itinerant character, mostly 4s character, hence the scattering rate
for this state is very small, and this state has very high mobility
despite the correlated nature of the gap. Due to finite k-point mesh,
this DOS appears somewhat spiky.
We can also take a look at the imaginary part of the green's
function. Recall that the imaginary part of the green's function,
divided by -pi, gives the DOS. So, plotting the even-numbered columns
in the MnO.gc1 one, we can get the DOS of individual d orbitals (eg and
t2g). The plot is
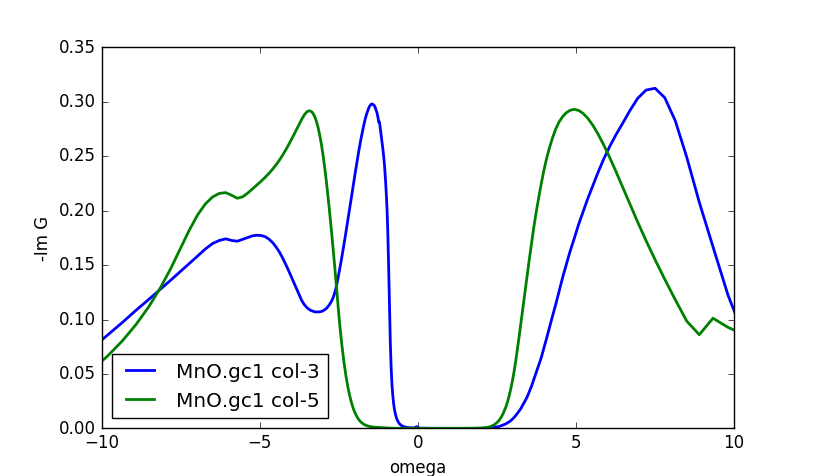 Notice that column 3 is the eg, and column 5 the t2g DOS.
In this plot it is even more clear that the lower Hubbard band is below
-4eV, and that the first valence excitation of the eg-states is split
away, making a singlet between the oxygen states and the two eg
orbitals.
Notice that it is exactly this type of screening (hybridization screening) which reduces the low
energy Coulomb interaction, and therefore if one simulates a Hubbard
model for MnO, one needs to take much smaller U. Within our embedded
method, the Coulomb repulsion will thus always be large compared to
model calculations, as such screening very efficiently reduces
interaction in the solid.
Notice that column 3 is the eg, and column 5 the t2g DOS.
In this plot it is even more clear that the lower Hubbard band is below
-4eV, and that the first valence excitation of the eg-states is split
away, making a singlet between the oxygen states and the two eg
orbitals.
Notice that it is exactly this type of screening (hybridization screening) which reduces the low
energy Coulomb interaction, and therefore if one simulates a Hubbard
model for MnO, one needs to take much smaller U. Within our embedded
method, the Coulomb repulsion will thus always be large compared to
model calculations, as such screening very efficiently reduces
interaction in the solid.
Note that the imaginary part of green's function and DOS use slightly
different normalization, therefore the sum of all green's functions
will typically produce slightly larger DOS than is computed in
case.cdos. This is because Green's functions are computed with
normalized projectors within a mufin-thin sphere (the integral of
spectral function is by construction exactly unity), while partial dos
usually uses unnormalized projector.
Another quantity of physical interest is the impurity
hybridization function. It is stored in the file MnO.dlt1, and its
imaginary part, which has the units of eV,
looks like the following:

The large peak below the Fermi level signals the hybridization of
eg states with the oxygen p states, as expected on the basis of
previous discussion.
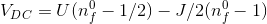
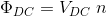
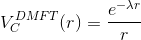 and the screening length is determined such that
and the screening length is determined such that

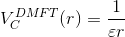
 Of course, the equation
Of course, the equation
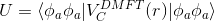 still needs to be satisfied.
still needs to be satisfied.